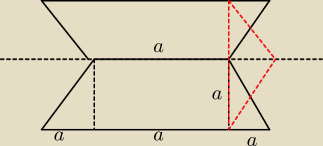
 W trapezie równoramiennym jedna z podstaw jest trzy razy dłuższa od drugiej. Bryła B1 powstała
z obrotu trapezu wokół krótszej podstawy,a bryła B2 powstała z obrotu trapezu wokół dłuższej
podstawy. Wyznacz stosunek objętnosci B1 i B2
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
tak to sobie wyobraziłem przypadek z B1 ( jakwidać na obrazku.)
i nie mam pojecia jak obliczyc objętosc tej bryły, myślałem ,nad takim pomyslem "na czerwono"
lecz wtedy stosunek tych brył był 1:1 ...
W trapezie równoramiennym jedna z podstaw jest trzy razy dłuższa od drugiej. Bryła B1 powstała
z obrotu trapezu wokół krótszej podstawy,a bryła B2 powstała z obrotu trapezu wokół dłuższej
podstawy. Wyznacz stosunek objętnosci B1 i B2
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
tak to sobie wyobraziłem przypadek z B1 ( jakwidać na obrazku.)
i nie mam pojecia jak obliczyc objętosc tej bryły, myślałem ,nad takim pomyslem "na czerwono"
lecz wtedy stosunek tych brył był 1:1 ...
 B1:
B1:
| 2 | ||
Vwalca − 2Vstożka = πr2H − | πr2 * H1 =
| |
| 3 |
| 2 | 2 | 7 | ||||
= πa2 * 3a − | πa2 * a = 3a3π − | a3π = | a3π | |||
| 3 | 3 | 3 |
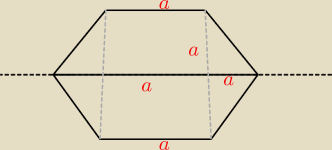 wersja B2
wersja B2
| 2 | ||
Vw+2Vs=a3π+ | a3π tak? | |
| 3 |

| 7 | 3 | 7 | |||||||||||||
= | * | = | ||||||||||||||
| 3 | 2 | 2 |
| 7 | ||
a odpowiedz mam |  | |
| 5 |
| 5 | ||
Vw + 2Vs = | a3π  | |
| 3 |
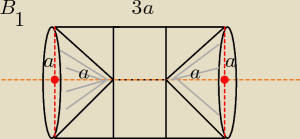 B1 −−− to walec z wydrążonymi na podstawach stożkami o tej samej objętości
V(B1) = V(walca ) − 2V(stożka)
wymiary walca: H= 3a , rw =a
wymiary stożków : h= a rst= rw= a
B1 −−− to walec z wydrążonymi na podstawach stożkami o tej samej objętości
V(B1) = V(walca ) − 2V(stożka)
wymiary walca: H= 3a , rw =a
wymiary stożków : h= a rst= rw= a
| 2 | ||
V(B1)= 3πa3 − | πa3 =.......
| |
| 3 |
| 2 | ||
V(B2)= πa3 + | πa3 =..........
| |
| 3 |
| V(B1) | |
=.........
| |
| V(B2) |



