moduł w module! hubcio: Wyznacz wszystkie wartości parametru m, mεR, dla których równanie ||x−10|−x|=m ma tylko jedno rozwiązanie

b.: najłatwiej na rysunku, sporządzając wykres funkcji po lewej stronie (łatwo stopniowo w kilku krokach nie jest trudne!)

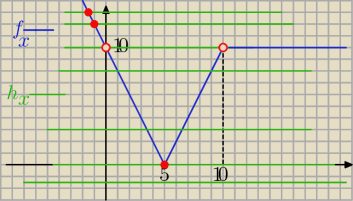
Eta: Można rozwiązać, wykorzystując wykresy funkcji po lewej i prawej stronie L= f(x)= | |x−10| −x| { | x−10 −x | dla x ≥10 => { 10 dla x ≥ 10 f(x)= { | −x +10 −x | dla x<10 => { 2 | x − 5| dla x <10 { 2x −10 dla x ≥5 i x<10 g(x) = 2|x−5 | = { −2x +10 dla x <5 i x< 10 i mamy: { 10 dla x≥10 f(x)= { 2x−10 dla 5≤ x < 10 { −2x+10 dla x <5 proste h(x) = m przecinają wykres f(x) tylko w jednym punkcie , gdy m€ ( 10, ∞) u {0} odp: równanie ma tylko jedno rozwiązanie dla parametru m€ ( 10,∞0 U {0}

Eta: poprawiam zapis m€(10, ∞) U {0}