adawdawd karolajnn: Dla jakich wartości parametru m równanie ma dwa pierwiastki rzeczywsite różnych znaków x² −2(m−1)x +2m+1=0 Δ≥0 a≠0 x1 x2<0 Δ= 4m² −16 m∊ <0;∞) v <4;∞) x1x2<0⇔m∊(−∞;0,5) Odpowiedź (−nieskoń.; 0,5) Mam błąd w delcie, mógłby ktoś ją dla mnie rozpisać/

Przetłumacz ;): Δ>=0 ⇔ 4(m−1)² − 4(2m+1) ⇔4m²−8m+4 −8m−4⇔4m²−16m⇔m²=4⇒ m=2 m=−2

karolajnn: Dlaczego nie moge wyciagnac przed nawias 4m i będzie 4m(m²−4) i wtedy 4m=0 lub m²−4=0 i wtedy wychodzi ze m nalezy(0;niesk) i tak samo tylko że od 4.

Artur: Dobrze karolajnn,

Artur: Przetłumacz zgubił m przy 4 w przedostatnim działaniu

Artur: 4m(m−4) bez m²

karolajnn: Ale jemu wyszedł dobry wynik.... m=2 v m=−2 a mi wychodzi zupełnie inaczej mógłby ktoś mi to wytłumaczyć ?

karolajnn:

karolajnn: jednak jemu niekonieczne wyszedl dobry wynik, jednak delta musi miec cos z minusem zeby zgadzało sie z odpowiedzi.

adax: Δ=[−2(m−1)] ² − 4*(2m+1)= 4(m−1)² −8m−4= 4(m²−2m+1)−8m−4=4m²−8m+4−8m−4=4m²−16m 4m²−16m=0 4m²=16 m=2 v −2

Artur: adax skąd z tego 4m²−16m=0 wzieło Ci się to 4m²=16 Co z m przy 16

karolajnn: własnie

adax: a przepraszam mój błąd powinno być 4m2−16m=0 4m(m−4)=0 x₁=0 x₂=4 a jak powinno wyjść?

karolajnn: Mam obliczyć kiedy delta jest ≥0 wychodzą liczby dodatnie lub 0. A musi być coś ujemnego mniejszego od 0,5 żeby wszystko sie zgadzało ..

karolajnn: Na górze masz równanie i polecenie.

bezskutecznie: z delty 4m(m−4)>0 czyli <−∞,0)u(4,∞) i wzory vietea c/a<0 2m+1<0 m<−1/2

bezskutecznie: zapomniałem dodać żebyć wzięła część wspólną czyli m<1/2 (ostatecznie) [mam nadzieje, że to nie klasa maturalna bo jak czytam takie pierdoły to sie aż łapię za głowę!]

karolajnn: 4m>0 m>0 m∊(0;∞) nie sądzisz ?

adax: c/a<0 2m+1<0 2m<−1 m<−1/2 część wspólna m<−1/2

karolajnn: tak tak tak, ale musze miec przeciez delte, która musi być od −∞, żeby ta czesc wspol;na była

adax: deltę już jest obliczona m∊ <0;∞) v <4;∞)

karolajnn: rozwiązaniem jest częśc wspólna delty i x1x2 z założeniami. Jak mogą mieć część wspólna, jeśli delta jest powyżej 0.

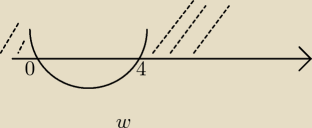
bezskutecznie: na rysunku x dla których nierówność delty jest spełniona, dodaj do tego warunek c/a<0 czyli x<1/2 i wyjdzie część wspólna x<1/2 obyśmy się więcej nie spotkali