 a) x + 2 y − 2 = 0
2 x − y − 4 = 0
−−−−−−−−−−−−
x = 2 − 2y
2*( 2 − 2y) − y = 4
4 − 4y − y = 4
− 5 y = 0
y = 0
x = 2 − 2*0 = 2
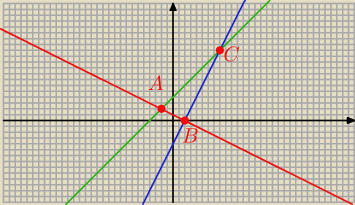
B = ( 2; 0)
========
x + 2 y − 2 = 0
x − y + 4 = 0
−−−−−−−−−−−−− odejmujemy stronami
3 y = 6
y = 2
x = y − 4 = 2 − 4 = − 2
A = ( − 2; 2)
==========
2 x − y − 4 = 0
x − y + 4 = 0
−−−−−−−−−−−− odejmujemy stronami
x = 8
y = x + 4 = 8 + 4 = 12
C = ( 8 ; 12)
==========
c)
→
BA = [ − 2 − 2; 2 − 0 ] = [ −4; 2 ]
→
BC = [ 8 − 2; 12 − 0 ] = [ 6 ; 12 ]
Iloczyn skalarny
→ →
BA o BC = − 4*6 + 2*12 = − 24 + 24 = 0
więc te wektory są prostopadle , czyli boki AB i BC są prostopadłe, a to oznacza,że
Δ ABC jest prostokątny.
II sposób − tw. Pitagorasa
b) Pole Δ ABC
Mamy
I BA I = I AB I = √(−4)2 + 22 = √16 + 4 = √20 = √4*5 = 2√5
I BC I = √62 + 122 = √ 36 + 144 = √180 = √36*5 = 6√5
więc
P = 0,5 *I AB I*I BC I = 0,5*2√5*6√5 = 6*5 = 30 [ j2]
a) x + 2 y − 2 = 0
2 x − y − 4 = 0
−−−−−−−−−−−−
x = 2 − 2y
2*( 2 − 2y) − y = 4
4 − 4y − y = 4
− 5 y = 0
y = 0
x = 2 − 2*0 = 2
B = ( 2; 0)
========
x + 2 y − 2 = 0
x − y + 4 = 0
−−−−−−−−−−−−− odejmujemy stronami
3 y = 6
y = 2
x = y − 4 = 2 − 4 = − 2
A = ( − 2; 2)
==========
2 x − y − 4 = 0
x − y + 4 = 0
−−−−−−−−−−−− odejmujemy stronami
x = 8
y = x + 4 = 8 + 4 = 12
C = ( 8 ; 12)
==========
c)
→
BA = [ − 2 − 2; 2 − 0 ] = [ −4; 2 ]
→
BC = [ 8 − 2; 12 − 0 ] = [ 6 ; 12 ]
Iloczyn skalarny
→ →
BA o BC = − 4*6 + 2*12 = − 24 + 24 = 0
więc te wektory są prostopadle , czyli boki AB i BC są prostopadłe, a to oznacza,że
Δ ABC jest prostokątny.
II sposób − tw. Pitagorasa
b) Pole Δ ABC
Mamy
I BA I = I AB I = √(−4)2 + 22 = √16 + 4 = √20 = √4*5 = 2√5
I BC I = √62 + 122 = √ 36 + 144 = √180 = √36*5 = 6√5
więc
P = 0,5 *I AB I*I BC I = 0,5*2√5*6√5 = 6*5 = 30 [ j2]
| − 2 + 2 | 2+0 | |||
więc środek okręgu S = ( | ; | ) = ( 0 ; 1) | ||
| 2 | 2 |