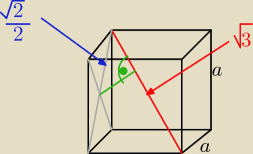
Homer: Dany jest sześcian o krawędzi a=1. Ze środka ściany sześcianu poprowadzono prostą prostopadłą do przekątnej sześcianu. Oblicz długości odcinków, na jakie ta prosta podzieliła przekątną sześcianu. Taki zrobiłem rysunek. Ale jak to policzyć ?

bezskutecznie: zauważ, że przekątna sześcianu z przekątną ściany bocznej i krawędzią podstawy tworzą trójkąt, a szukana odległość wyznacza trójkąt podobny

bezskutecznie: x 1 −−− = −− √2/2 √3 x=√6/6 zgadza się?

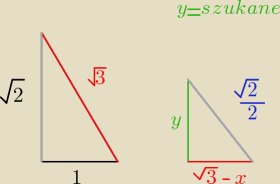
Homer: Zauważyłem to, ale mam chyba za mało wiadomych żeby to policzyć.zu

Homer: Możesz to narysować na trójkątach tak jak ja ? Bo nie widzę tego. Wynik masz dobry.

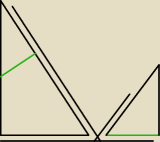
bezskutecznie: nie wiem jak sie pisze na rysunkach więc zaznaczyłem które boki są podobne, a przeciwprostokątna małego trójkątna to połowa przekątnej ściany bocznej

bezskutecznie: jeśli nadal nie widzisz podobieństwa to tyle jeszcze moge odpowiedzieć, że stosunek szukanej do przeciwprostokątnej małego trójkąta wynosi tyle co stosunek długości boku podstawy sześcianu do jego przekątnej

Homer: dzięki. Rozumiem