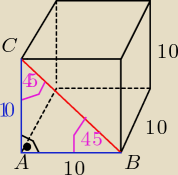
 ΔABC jest prostokątny i równoramienny
więc |AB|= AC|= 10
Takim graniastosłupem jest sześcian o krawędzi a= 10
V= a3 =.......
Pc= 6a2=.......
ΔABC jest prostokątny i równoramienny
więc |AB|= AC|= 10
Takim graniastosłupem jest sześcian o krawędzi a= 10
V= a3 =.......
Pc= 6a2=.......
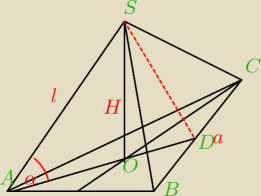 Prawidłowy trójkątny to znaczy że trójkąt równoboczny w podstawie. Skoro trójkąt równoboczny to
znaczy że wysokość podstawy:
hpodstawy = a √32 = 5√3
Skoro trójkąt równoboczny to wysokości w podstawie dzielą się dzielą się w stosunku 2:1 czyli
|AO| = 23|AD|
czyli:
|AO| = 10 √33
skoro mamy odcinek |AO| to wychodzimy z funkcji trygonometrycznych:
cosα = |AO|H
a α = 45o więc cosα = √22
z tego wyliczamy H. Pole podstawy obliczamy ze wzoru P = a2 √34 i obliczamy objętość.
Następnie z pitagorasa ( |OD|2 + H2 = |SD|2) obliczamy wysokość ściany bocznej i liczymy
Pole powierzchni całkowitej ze wzoru Pc = Pp + 3Pb
Prawidłowy trójkątny to znaczy że trójkąt równoboczny w podstawie. Skoro trójkąt równoboczny to
znaczy że wysokość podstawy:
hpodstawy = a √32 = 5√3
Skoro trójkąt równoboczny to wysokości w podstawie dzielą się dzielą się w stosunku 2:1 czyli
|AO| = 23|AD|
czyli:
|AO| = 10 √33
skoro mamy odcinek |AO| to wychodzimy z funkcji trygonometrycznych:
cosα = |AO|H
a α = 45o więc cosα = √22
z tego wyliczamy H. Pole podstawy obliczamy ze wzoru P = a2 √34 i obliczamy objętość.
Następnie z pitagorasa ( |OD|2 + H2 = |SD|2) obliczamy wysokość ściany bocznej i liczymy
Pole powierzchni całkowitej ze wzoru Pc = Pp + 3Pb
 ........ sorry przeczytałam czworokątny
........ sorry przeczytałam czworokątny  a Ty Atime ....też źle ......... bo to nie ostrosłup, tylko graniastosłup
a Ty Atime ....też źle ......... bo to nie ostrosłup, tylko graniastosłup  i mamy remis w pomyłkach 1: 1
i mamy remis w pomyłkach 1: 1
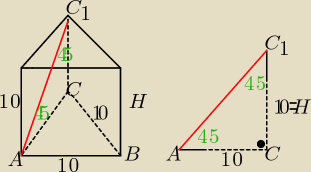 a= 10 −−− dł. krawędzi podstawy
H= 10 −−− dł. wysokości graniastosłupa
a= 10 −−− dł. krawędzi podstawy
H= 10 −−− dł. wysokości graniastosłupa
| a2√3 | ||
V= Pp*H= | *H=......... podstaw dane
| |
| 4 |
| a2√3 | ||
PC= 2Pp + 3a*H = 2* | +3aH=........
| |
| 4 |
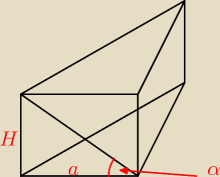 czyli tgα = Ha
tg45o = 1 więc a = H czyli ścianami bocznymi są kwadraty. Pole podstawy obliczasz ze wzoru
a2√34 a objętość V = Pp * H
Pole boczne to jest pole podstawy + 3 razy pole kwadratu o boku a.
Przepraszam za poprzedni błąd, nie doczytałem i myślałem, że chodzi o ostrosłup
czyli tgα = Ha
tg45o = 1 więc a = H czyli ścianami bocznymi są kwadraty. Pole podstawy obliczasz ze wzoru
a2√34 a objętość V = Pp * H
Pole boczne to jest pole podstawy + 3 razy pole kwadratu o boku a.
Przepraszam za poprzedni błąd, nie doczytałem i myślałem, że chodzi o ostrosłup 