dero2005 pomozesz?
magnum2020: Oblicz objetosc i pole powierzchni calkowitej czworoscianu foremnego ktorego krawedz ma dlugosc
6√2
zad.2
Oblicz objetosc ostrosłupa prawidłowego trójkatnego, w ktorym wysokosc jest rowna 24, a
wysokosc sciany bocznej wynosi 26
zad.3
Oblicz pole powierzchni i objetosc ostrosłupa prawidłowego czworokatnego, ktorego krawedz
podstawy ma długosc 5 a krawedz boczna 8.
zad.4
Podstawa ostrosłupa jest trójkat prostokatny o przyprostokatnych 16 i 12. Kazda krawedz boczna
ostrosłupa jest nachylona do płaszczyzny podstawy po katem 60stopni. Oblicz objetosc
ostrosłupa.
5 kwi 17:45
dero2005:

W czworościanie wszystkie krawędzie są równe
z trójkąta podstawy (po prawej stronie)
| | a√3 | | 6√2*√3 | |
hp = |
| = |
| = 3√2*√3 = 3√6
|
| | 2 | | 2 | |
z trójkąta wysokości, 2/3 wysokości podstawy i krawędzi bocznej (w środku) Tw Pitagorasa
h
2 = a
2 − (
23h
p)
2
h
2 = (6
√2)
2 − (
23*3
√6)
2
h
2 = 72 − 24 = 48
h =
√48 = 4
√3
pole podstawy
| | a2√3 | | (3√6)2*√3 | |
Pp = |
| = |
| = 18√3
|
| | 4 | | 4 | |
pole całkowite
P
c = 4*P
p = 4*18
√3 = 72
√3
objętość
V =
13P
p*h =
13*18
√3*4
√3 = 72
Można też zrobić na skróty wg wzorów
P
c = a
2√3 = (6
√2)
2*
√3 = 72
√3
| | a3√2 | | (3√2)3*√2 | |
V = |
| = |
| = 72 |
| | 12 | | 12 | |
6 kwi 08:09
dero2005:
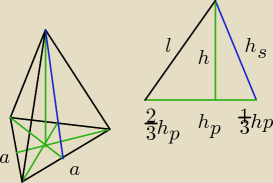
h = 24 wysokość
h
s = 26 wysokość ściany
trójkąt po prawej stronie (tw Pitagorasa)
(h
s)
2 = h
2 + (
13h
p)
2
h
s2 = h
2 +
19h
p2
h
p2 = 9h
s2 − 9h
2
h
p2 = 9(26
2−24
2) = 900
h
p = 30
a − krawędź podstawy
a = 20
√3
P
p − pole podstawy
P
p = 300
√3
V− objętość
V =
13P
p*h =
13*300
√3*24 = 2400
√3 [j
3]
6 kwi 17:36
dero2005:
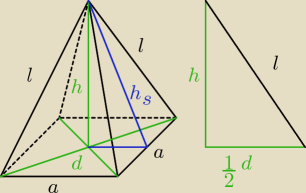
a = 5
l = 8
d
2 = 2a
2
d = a
√2 = 5
√2
| | 103 | | √206 | |
h = √l2 − (12d)2 = √ |
| = |
|
|
| | 2 | | 2 | |
| | √231 | |
hs = √(a2)2 + h2 = |
|
|
| | 2 | |
| | √231 | |
Pb = 2ahs = 2*5* |
| = 5√231
|
| | 2 | |
P
p = a
2 = 5*5 = 25
P
c = P
p + P
b = 25 + 5
√231
| | √206 | | 25 | |
V = 13*Pp*h = 13*25* |
| = |
| √206
|
| | 2 | | 6 | |
6 kwi 19:52
dero2005:
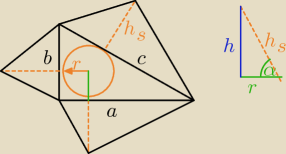
zad 4)
na rysunku ostrosłup w rozwinięciu
dane:
a = 16
b = 12
α = 60
o
Spodek wysokości ostrosłupa pokrywa się ze środkiem okręgu wpisanego
c − przeciwprostokątna
c
2 = a
2 + b
2
c
2 = 16
2 + 12
2 = 400
c = 20
P
p − pole podstawy
P
p =
r2(a+b+c) =
r2(16+12+20) = 24r
24r = 96
r = 4
wg trójkąta po prawej stronie
h = r
√3 = 4
√3
V =
13*P
p*h =
13*96*4
√3 = 128
√3
V = 128
√3
7 kwi 17:50
 W czworościanie wszystkie krawędzie są równe
z trójkąta podstawy (po prawej stronie)
W czworościanie wszystkie krawędzie są równe
z trójkąta podstawy (po prawej stronie)
 h = 24 wysokość
hs = 26 wysokość ściany
trójkąt po prawej stronie (tw Pitagorasa)
(hs)2 = h2 + (13hp)2
hs2 = h2 + 19hp2
hp2 = 9hs2 − 9h2
hp2 = 9(262−242) = 900
hp = 30
a − krawędź podstawy
h = 24 wysokość
hs = 26 wysokość ściany
trójkąt po prawej stronie (tw Pitagorasa)
(hs)2 = h2 + (13hp)2
hs2 = h2 + 19hp2
hp2 = 9hs2 − 9h2
hp2 = 9(262−242) = 900
hp = 30
a − krawędź podstawy
 a = 5
l = 8
d2 = 2a2
d = a√2 = 5√2
a = 5
l = 8
d2 = 2a2
d = a√2 = 5√2
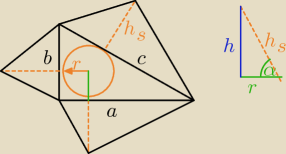 zad 4)
na rysunku ostrosłup w rozwinięciu
dane:
a = 16
b = 12
α = 60o
Spodek wysokości ostrosłupa pokrywa się ze środkiem okręgu wpisanego
c − przeciwprostokątna
c2 = a2 + b2
c2 = 162 + 122 = 400
c = 20
Pp − pole podstawy
zad 4)
na rysunku ostrosłup w rozwinięciu
dane:
a = 16
b = 12
α = 60o
Spodek wysokości ostrosłupa pokrywa się ze środkiem okręgu wpisanego
c − przeciwprostokątna
c2 = a2 + b2
c2 = 162 + 122 = 400
c = 20
Pp − pole podstawy