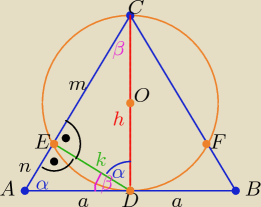
Zadanie Agata: Umrę jak tego nie zrobię Agata: Rozwiązuję to zadanie już kolejny raz i za każdym razem wychodzi mi coś innego 1.41. W trójkącie równoramiennym ABC ( I AC I = I BC I ) długość wysokości CD wynosi h. Okrąg, którego średnicą jest ta wysokość, przecina boki trójkąta w punktach E i F. Oblicz pole tego trójkąta wiedząc,że I EC I : I AE I = I FC I : I BF I = m:n

och nie!:

Eta: P(ABC)= a*h |∡DEC|=90^o −−− kąt wpisany oparty na średnicy trójkąty DAE i DEC są prostokątne i podobne z cechy (kkk)

	k		m
to:		=		⇒ k2=mn
	n		k

z tw. Pitagorasa w trójkącie DEC:

	h2
h2=m2+k2 ⇒h2=m2+mn ⇒ h2= m(m+n) ⇒ (*) m+n=
	m

z tw. o stycznej i siecznej : |AD|²=|AC|*|AE| , |AC|= n+m , |AE|=n zatem: a²=(m+n)*n

	h2		n
a2=		*n ⇒ a= h*√		, a>0
	m		m

	n
Odp: P(ABC)= a*h ⇒ P= h2√		[j2]
	m

Zadanie czekało na rozwiązanie..........ponad 4 lata

Eta: Ciekawe co z Agatą ? ..... przez tak długi czas

use: skąd wiesz że 4 lata ?

Eta: @use podświetl datę pierwszego postu

use: ale bajer, nie wiedziałem