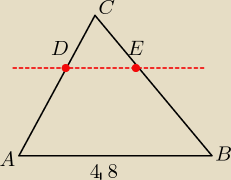
Podobieństwo Pietrek: W trójkącie ABC, /AB/=4,8dm, poprowadzono odcinek DE równoległy do boku AB, (D należy do AC, E należy do CB). Pole trójkata DEC jest równe 1dm2, a pole trapezu ABED− 8dm2. Oblicz długosć odcinka DE.

dobra rada: P(ΔABC)= 1+8= 9 dm² ΔDEC ~ Δ ABC w skali k >0 to:

P(ΔDEC)		1
	= k2=
P(ΔABC)		9

	1
k=		−−−− skala podobieństwa
	3

	1
|DE|=		*|AB|=.........
	3

Pietrek: Dziękuje

Pietrek: a dlaczego tam jest k² ?

Pietrek: Przypuszczam ze dlatego, że to pole? wiec kwadrat