lol Damian: mozecie mi wytlumaczyc roznice miedzy wariacjami i kombinacjami na jakims latwym przykladzie?

M:

M:

wredulus_pospolitus: jakby ktoś z potomnych się nad tym zastanawiał: 1. W wariacji i w kombinacji mamy na celu z jakiegoś zbioru wybrać ileś elementów. 2. Różnica pomiędzy wariacją a kombinacją jest taka ... czy bierzemy pod uwagę kolejność w jakim wybraliśmy te elementy. Przykład nr 1: W klasie mam 20 uczniów. Wybieramy 'trójkę klasową'. Na ile sposobów możemy to uczynić. Odpowiedź:: Zauważmy, że tutaj nie ważne jest czy Franek został wybrany jako pierwszy czy jako ostatni. Istotne jest tylko czy został wybrany czy też nie. Związku z tym kolejność nie jest istotna. Stąd:

20 3		20*19*18
	=
		3!

Przykład nr 2: W klasie mam 20 uczniów. Wybieramy 'trójkę klasową', w skład której wchodzi: przewodniczący, wice, skarbnik. Na ile sposobów możemy to uczynić. Odpowiedź:: Zauważmy, że tutaj istotne jest czy Franek został wybrany jako przewodniczący (pierwszy) czy jako skarbnik (ostatni). Czyli nie tylko jest istotne jest tylko czy został wybrany czy też nie, ale także do jakiej roli (który w kolejności). Stąd:

20!
	= 20*19*18
17!

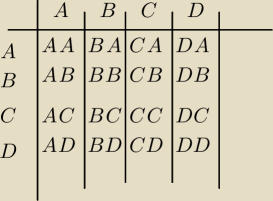
Leszek: można tak to wytłumaczyć: dany jest zbiór elementów : X = {A,B,C,D} 1) tworzymy dwuelementowe podzbiory czyli pary ale takie ,że mogą elementy zbioru X powtarzać się i występować w różnej kolejności : (A,B) (A,C) (A,D) (A,A) (B,B) (C,C) (D,D) (B,A) (B,C) (B,D) ......( patrz tabelka) sa to wówczas wariacje z powtórzeniami. ich ilość obliczamy na podstawie wzoru : W = n^k, n −ilość elementów zbioru X , k −ilość elementów w podzbiorze. 2) tworzymy dwuelementowe podzbiory ale w których elementy nie powtarzają się czyli odrzucamy (A,A) (B,B) (C,C) (D,D) , są to wariacje bez powtórzeń

	n!
ich ilość obliczamy na podstawie wzoru: V =
	(n−k)!

3) tworzymy dwuelementowe podzbiory, ale pozbiór (A,B) = (B,A) jest jednym podzbiorem zostaja więc : (A,B) (A,C) (A,D) (B,C) (B,D) (C,D) , sa to kombinacje

	n!
ich ilość obliczmy : C =
	k!(n−k)!

Podstawy Geometrii: Dziękuje .Przyda się ,do rozważań jak juz będzie po wszystkim . Mam tylko taką nadzieję że to nie będzie trwać 21 lat tak jak wojna pomiędzy Rosją a Szwecją i bardzo szybko zapanuje pokój .