Parametr
;): Określ liczbę pierwiastków równania 2x
2 − 5|x| − m = 0 w zależności od wartości parametru m.
I teraz prosiłbym o sprawdzenie czy dobrze to zrobiłem.
m=0⇒3 rozw.
m∊(0,
∞)⇒2 rozw.
4 kwi 20:43
Godzio:
Jest ok

4 kwi 20:44
;): Okej dziekuję

Biorę się za kolejne.
4 kwi 20:49
;):
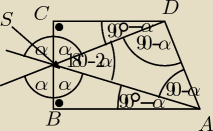
Dany jest rapez prostokątny ABCD o podstawach AB i CD w którym boki AB i BC są prostopadłe.
Dwusieczne kątów A i D przecinają się w punkcie S leżącym na boku BC. Wykaż że |BS| = |SC|
Teraz jak to mam wykazać? Wychodzi że |DS| = |AS| bo trójkąt ASD jest równoramienny.
| | |DS| | | |CS| | |
Trójkąty CSD i ABS są podobne cecha KKK układam proporcje |
| = |
| skoro |
| | |AS | | |BS| | |
|DS| = |AS| to |CS| = |AS|.
Nie wiem czy dobrze to wykazałem gdyby ktoś mógł zerknąć i poprawić.
4 kwi 21:17
Godzio :
Czekałem aż wrzucisz to zadanie

Po czym wnioskujesz że |∡SDA| = |∡DAS|
4 kwi 21:20
;): Przy wierzchołku S oznaczyłem że jest to 2α a |CB| dzieli ∡S na α i α skąd wnioskuję że
∡CDS = 90 −α tak samo ∡BAS a skoro |DS| jest dwusieczna to ∡SDA i ∡DAS są takie same. Ech nie
nawidzę takich rzeczy wykazywać

4 kwi 21:27
Godzio :
Ale moim zdaniem sobie zbytnio ułatwiłeś, założyłeś sobie że prosta BC dzieli kąt 2α na równe
części, a moim zdaniem to nie jest poprawne. Byłoby tak wtedy gdybyś wiedział że S dzieli bok
BC na 2 równe części, a póki co masz to wykazać

4 kwi 21:32
kamis:
Musisz jedną rzecz udowodnić i jedną rzecz dorysować, w zasadzie dwie.
4 kwi 21:38
Godzio :
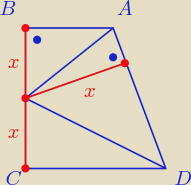
Przeczytaj sobie definicję dwusiecznej

4 kwi 21:46
;): Właśnie z góry sobie założyłem że |CB| jest dwusieczna ∡S Chwilkę muszę pomyśleć jak to zadanie
ugryźć

Nie lubie tego typu zadań.
4 kwi 21:50
;): Niestety Godziu przeczytałem ale nie rozumiem nadal...
4 kwi 22:09
Godzio :
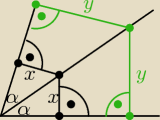
Dwusieczna jest zbiorem punktów równo odległych od ramion kąta
Teraz trochę rozjaśniłem ?
4 kwi 22:12
;): Za parę chwil napisze przeanalizuję wszystko ale teraz mi jest łatwiej myśleć dziekuje

4 kwi 22:16
;): No nareszcie zrozumiałem to wielkie dzieki
Godziu
Teraz za następne się biorę dam znać
co tam wyprodukuje
4 kwi 22:24
Godzio :
Ok

Też już sobie je przejże bo i tak muszę na środę zrobić ...
4 kwi 22:25
;): a = 8
b = −10
c = −52
? możesz sprawdzić czy dobrze

4 kwi 22:41
Godzio : Mi tak wyszło:
a = 4
b = −18
c = −20
4 kwi 22:55
;): może jak zawsze jakiegoś chochlika zrobiłem idę zerknąć jeszcze raz
4 kwi 23:02
Godzio :
Pomyliłem się w obliczeniach teraz zobaczyłem, powinno być:
a = −11
b = −3
c = 10
4 kwi 23:02
Godzio :
W(x) = x4 + 3x3 + ax2 + bx + c
P(x) = x2 + 3x − 10 = (x + 5)(x − 2)
⇒ W(−5) = 0, W(2) = 0 oraz W(−1) = −36
(1) 625 − 375 + 25a − 5b + c = 0 ⇒ 25a − 5b + c = − 250
(2) 16 + 24 + 4a + 2b + c = 0 ⇒ 4a + 2b + c = −40
(3) 1 − 3 + a − b + c = 0 ⇒ a − b + c = 2
(2) − (3) = 3a + 3b = −42 ⇒ a + b = − 14
(1) − (2) = 21a − 7b = −210 ⇒ 3a − b = −30
a + b = −14
3a − b = −30 +
−−−−−−−−−−−−
4a = −44
a = −11 ⇒ b = −3 ⇒ c = 10
4 kwi 23:04
;): Godziu
1 − 3 + a − b + c = −36

4 kwi 23:07
Godzio : ehhh

4 kwi 23:11
;): 25a − 5b + c = − 250
4a + 2b + c = −40
1 − 3 + a − b + c = −36⇒ a + c = −34 +b
24a − 4b = −216
3a + 3b = −6
6a − b = −54
a + b = −2 +
−−−−−−−−−−−−−−−−−−−−
7a = −56
a = −8
b= 6
c = −20
4 kwi 23:19
;): teraz jak się już gdzieś walnąłem to idę spać

4 kwi 23:24
Godzio :
Wszystko ok

4 kwi 23:27
;): No jeżeli tak to spróbuje kolejne heh

4 kwi 23:28
;): Masz może pomysł jakiś na to?

zapisałem tak
a
1 = a a
2 = ax q = x
log
a x log
ax x log
ax2 x Dobrze to zapisane jest?
4 kwi 23:41
Godzio :
log
ax, log
bx, log
cx, log
dx
a,ax,ax
2,ax
3
log
ax < −1
log
ax + log
bx = log
cx + log
dx
Tak mi wyszło:
O ile dobrze to rozumiem

4 kwi 23:42
;): to widzę że tak samo spróbuje dojść do Twojego wyniku

4 kwi 23:43
;): | 1 | | 1 | | 1 | | 1 | |
| + |
| = |
| + |
| |
| logxa | | logxax | | logxax2 | | logxax3 | |
log
xax = log
xa + log
xx
| 1 | | 1 | | 1 | | 1 | |
| + |
| = |
| + |
| |
| logxa | | logxa + 1 | | logxa + 2 | | logxa + 3 | |
log
xa=t
| 1 | | 1 | | 1 | | 1 | |
| + |
| = |
| + |
| |
| t | | t + 1 | | t + 2 | | t + 3 | |
I nie wiem czy dobrze myślę?

4 kwi 23:55
Godzio :
Zdaje się że tak

4 kwi 23:58
Godzio :
Ja już idę spać bo padam, a Ty się męcz

4 kwi 23:59
;): Jutro to ja Cie pomęczę kolejnymi zadankami znaczy nawet dzisiaj można powiedzieć

5 kwi 00:00
;): Dobranoc

5 kwi 00:01
;): (2t + 1) (t
2 + 5t +6) = (t
2 + t) (2t + 5)
4t
2 + 12t + 6 =0/:2
2t
2 + 6t + 3 =0
Δ=3
√Δ=
√3 t < −1
| | 3 + √3 | |
t1= − |
| wiec t2 nie liczę bo t < −1 |
| | 2 | |
5 kwi 00:14
;): f(x) = 2sinx + cos2x
f(x) = −2sin
2x + 2sinx + 1
t = sinx t∊<−1,1>
h(t) = −2t
2 + 2t +1
| | 1 | | 1 | |
h( |
| ) = 1 |
| → największa wartość bo a<0 |
| | 2 | | 2 | |
h(−1) = −3
h(1) = 1
5 kwi 18:03
;): | | a + b | | a − b)2 | |
Udowodnij że jeżeli a ≥ b > 0 to |
| − √ab ≥ |
| |
| | 2 | | 8a | |
5 kwi 19:29
Godzio:
Dzisiaj w szkole sobie to udowodniłem, za łatwo nie było

5 kwi 19:30
;): Weź spójrz na to bo już nie wytrzymuje z tym zadaniem

| a + b | | (a − b)2 | |
| − √ab ≥ |
| / 8a |
| 2 | | 8a | |
4a(a + b) − (a − b)
2 ≥ 8a
√ab
4a
2 + 4ab − a
2 + 2ab − b
2 ≥ 8a
√ab
3a
2 + 6ab − b
2 ≥ 8a
√ab /
2
9a
4 + 36a
2b
2 + b
4 + 36a
3b − 6a
2b
2 − 12ab
3 ≥ 64a
3b
9a
4 − 28a
3b + 30a
2b
2 −12ab
3 + b
4 ≥0
(a − b)
4 + 8a(a − b)
3 ≥0
(a − b)
3 (9a + b) ≥0
a ≥ b
c.n.u
5 kwi 19:31
Godzio:
Nieźle namotane

przed przed ostatnie przejście jest ok, to jest dobrze, ja zrobiłem w trochę
inny sposób

I trzeba w tym wypadku dawać znaki równoważności ⇔
5 kwi 19:37
;): A mógłbyś pokazać jak Ty to udowoniłeś

Właśnie tak namotałem że szok ale dobrze jest to
przejście czy nie? (a − b)
4 + 8a(a − b)
3
5 kwi 19:41
Godzio :
Na Wolframie pokazuje, że (a − b)
3(9a
− b) ale na jedno wyjdzie
W sumie to ja też namotałem

| a + b | | (a − b)2 | |
| − √ab ≥ |
| / * 2 ⇔ |
| 2 | | 8a | |
| | (a − b)2 | |
a − 2√ab + b ≥ |
| ⇔ |
| | 4a | |
| | (√a − √b)2(√a + √b)2 | |
(√a − √b)2 − |
| ≥ 0 ⇔ |
| | 4a | |
| | (√a + √b)2 | |
(√a − √b)2(1 − |
| ) ≥ 0 ⇔ |
| | 4a | |
(
√a −
√b)
2(4a − (
√a +
√b)
2) ≥ 0 ⇔
(
√a −
√b)
2(4a − a − 2
√ab − b) ≥ 0 ⇔
(
√a −
√b)
2(3a − 2
√ab − b) ≥ 0 ⇔
(
√a −
√b)
2(a − b + 2(a −
√ab) ≥ 0 ⇔
(
√a −
√b)
2(a − b + 2
√a(
√a −
√b)) ≥ 0
bo a ≥ b > 0 ⇒
√a −
√b ≥ 0, a − b ≥ 0
5 kwi 19:44
;): Tak właśnie chochlika zrobiłem tam przez nie uwagę

Fajnie to udowodniłeś a ja jakoś boje się
na pierwiastkach bawić więc jak zawsze do kwadratu podnoszę

Ale to zadanie chyba ciężkawe
nawet było
5 kwi 19:54
;): Jej rzeczywiście można to było Wolframem sprawdzić nawet nie pomyślałem o tym sam się musiałem
głowić jak to przekształcić aż mózg mi siadł

5 kwi 19:57
;): Godziu wiesz może jak zrobić to 6 zadanie?
5 kwi 19:58
Godzio :
Musiałbym chwilę pomyśleć

5 kwi 20:00
;): Okej mi się nie spieszy a chciałbym zobaczyć jak powinno wyglądać to zadanie

5 kwi 20:01
Godzio :
Kompletnie nie umiem działać na wektorach, wszystko sobie porozpisywałem i mi coś wyszło tylko
nie wiem jakie wierzchołki mi powychodziły ...
5 kwi 20:22
;): Wiesz chyba nie tylko Ty nie lubisz wektorów wogóle nie umiem się nimi posługiwać
5 kwi 20:31
Godzio :
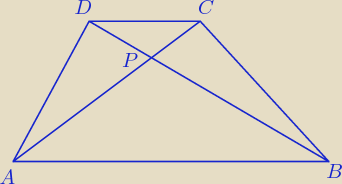
Takie mam rozwiązanie, ale nie odpowiadam za nie

Wektory [a,b] , [c,d] są równoległe gdy ac + bd = 0
CD = [10 − x
C, −9 − y
C] AB = [12,21] CB = [0,13] = [x
B − x
C, y
B − y
C]
Mamy wektor AB jest on równoległy co wektora CD więc zachodzi warunek:
(10 − x
C) * 12 − (9 + y
C) * 21 = 0
120 − 12x
C − 189 − 21y
C = 0
12x
C + 21y
C + 69 = 0 /:3
4x
C + 7y
C + 23 = 0
(1) x
B − x
A = 12
(2) y
B − y
A = 21
(3) x
B − x
C = 0
(4) y
B − y
C = 13
(1) − (3) = x
C − x
A = 12
(2) − (4) = y
C − y
A = 8
Wektor AC = [12,8] ,
|CP| =
√9 + 4 =
√13
|AP| = |AC| − |CP| = 4
√13 −
√13 = 3
√13
|AB| = 3
√5 * 13
| | |AP| | | 1 | |
ABP ~ PDC ⇒ k = |
| = 3 ⇒ |DC| = |
| |AB| = √65 |
| | |CP| | | 3 | |
65 = (x
C − 10)
2 + (y
C + 9)
2
4x
C + 7y
C + 23 = 0
Z tego wychodzi C(3,−5) lub C(17,−13)
A(−9,−13)
lub
A(5,−21)
B(3,8)
lub
B(17,0)
Odp: A(−9,−13), B(3,8), C(3,−5) lub A(5,−21) B(17,0) C(17,−13)
5 kwi 20:35
;): To może 9 jeżeli tak zerkniesz?

5 kwi 20:36
;): Oo nie zauważyłem rozwiązania będę musiał się nauczyć operować na wektorach a teraz zerknę na
Twoje rozwiazanie

5 kwi 20:39
;): Wykaż, że jeżeli, x + y = 4 to x
3 + y
3 ≥16
znalazłem takie zadanie

5 kwi 22:32
;): (x + y) (x2 − xy + y2) ≥16
4(x2 − xy + y2) ≥16
y = 4 − x
f(x) = 4(x2 + x2 − 4x + x2 − 8x + 16)
f(x) = 4(3x2 − 12x + 16)
f(x) = 12x2 − 48x + 64
xw = 2
f(2) = 48 − 96 + 64
f(2) = 16 → fmin = 16 dla x = 2
czyli x3 + y3 ≥16 c.n.w
5 kwi 22:45
;): Prosiłbym o sprawdzenie tego zadnia z góry dziękuję
5 kwi 22:53
Godzio :
Wydaje się być w porządku

5 kwi 22:55
;): Okej dziękuję

Właśnie się zastanawiałem czy mogłoby być też tak?
x
2 − xy + y
2 ≥4
x
2 + x
2 − 4x + x
2 − 8x + 16 ≥4
3x
2 − 12x + 12 ≥0
x
2 − 4x + 4 ≥0
(x − 2)
2 ≥0 x∊R
5 kwi 23:02

 Biorę się za kolejne.
Biorę się za kolejne.
 Dany jest rapez prostokątny ABCD o podstawach AB i CD w którym boki AB i BC są prostopadłe.
Dwusieczne kątów A i D przecinają się w punkcie S leżącym na boku BC. Wykaż że |BS| = |SC|
Teraz jak to mam wykazać? Wychodzi że |DS| = |AS| bo trójkąt ASD jest równoramienny.
Dany jest rapez prostokątny ABCD o podstawach AB i CD w którym boki AB i BC są prostopadłe.
Dwusieczne kątów A i D przecinają się w punkcie S leżącym na boku BC. Wykaż że |BS| = |SC|
Teraz jak to mam wykazać? Wychodzi że |DS| = |AS| bo trójkąt ASD jest równoramienny.
 Po czym wnioskujesz że |∡SDA| = |∡DAS|
Po czym wnioskujesz że |∡SDA| = |∡DAS|


 Przeczytaj sobie definicję dwusiecznej
Przeczytaj sobie definicję dwusiecznej 
 Nie lubie tego typu zadań.
Nie lubie tego typu zadań.
 Dwusieczna jest zbiorem punktów równo odległych od ramion kąta
Teraz trochę rozjaśniłem ?
Dwusieczna jest zbiorem punktów równo odległych od ramion kąta
Teraz trochę rozjaśniłem ?

 Teraz za następne się biorę dam znać
co tam wyprodukuje
Teraz za następne się biorę dam znać
co tam wyprodukuje
 Też już sobie je przejże bo i tak muszę na środę zrobić ...
Też już sobie je przejże bo i tak muszę na środę zrobić ...






 zapisałem tak
a1 = a a2 = ax q = x
loga x logax x logax2 x Dobrze to zapisane jest?
zapisałem tak
a1 = a a2 = ax q = x
loga x logax x logax2 x Dobrze to zapisane jest?









 przed przed ostatnie przejście jest ok, to jest dobrze, ja zrobiłem w trochę
inny sposób
przed przed ostatnie przejście jest ok, to jest dobrze, ja zrobiłem w trochę
inny sposób  I trzeba w tym wypadku dawać znaki równoważności ⇔
I trzeba w tym wypadku dawać znaki równoważności ⇔
 Właśnie tak namotałem że szok ale dobrze jest to
przejście czy nie? (a − b)4 + 8a(a − b)3
Właśnie tak namotałem że szok ale dobrze jest to
przejście czy nie? (a − b)4 + 8a(a − b)3

 Fajnie to udowodniłeś a ja jakoś boje się
na pierwiastkach bawić więc jak zawsze do kwadratu podnoszę
Fajnie to udowodniłeś a ja jakoś boje się
na pierwiastkach bawić więc jak zawsze do kwadratu podnoszę Ale to zadanie chyba ciężkawe
nawet było
Ale to zadanie chyba ciężkawe
nawet było



 Takie mam rozwiązanie, ale nie odpowiadam za nie
Takie mam rozwiązanie, ale nie odpowiadam za nie  Wektory [a,b] , [c,d] są równoległe gdy ac + bd = 0
CD = [10 − xC, −9 − yC] AB = [12,21] CB = [0,13] = [xB − xC, yB − yC]
Mamy wektor AB jest on równoległy co wektora CD więc zachodzi warunek:
(10 − xC) * 12 − (9 + yC) * 21 = 0
120 − 12xC − 189 − 21yC = 0
12xC + 21yC + 69 = 0 /:3
4xC + 7yC + 23 = 0
(1) xB − xA = 12
(2) yB − yA = 21
(3) xB − xC = 0
(4) yB − yC = 13
(1) − (3) = xC − xA = 12
(2) − (4) = yC − yA = 8
Wektor AC = [12,8] ,
|CP| = √9 + 4 = √13
|AP| = |AC| − |CP| = 4√13 − √13 = 3√13
|AB| = 3√5 * 13
Wektory [a,b] , [c,d] są równoległe gdy ac + bd = 0
CD = [10 − xC, −9 − yC] AB = [12,21] CB = [0,13] = [xB − xC, yB − yC]
Mamy wektor AB jest on równoległy co wektora CD więc zachodzi warunek:
(10 − xC) * 12 − (9 + yC) * 21 = 0
120 − 12xC − 189 − 21yC = 0
12xC + 21yC + 69 = 0 /:3
4xC + 7yC + 23 = 0
(1) xB − xA = 12
(2) yB − yA = 21
(3) xB − xC = 0
(4) yB − yC = 13
(1) − (3) = xC − xA = 12
(2) − (4) = yC − yA = 8
Wektor AC = [12,8] ,
|CP| = √9 + 4 = √13
|AP| = |AC| − |CP| = 4√13 − √13 = 3√13
|AB| = 3√5 * 13




 Właśnie się zastanawiałem czy mogłoby być też tak?
x2 − xy + y2 ≥4
x2 + x2 − 4x + x2 − 8x + 16 ≥4
3x2 − 12x + 12 ≥0
x2 − 4x + 4 ≥0
(x − 2)2 ≥0 x∊R
Właśnie się zastanawiałem czy mogłoby być też tak?
x2 − xy + y2 ≥4
x2 + x2 − 4x + x2 − 8x + 16 ≥4
3x2 − 12x + 12 ≥0
x2 − 4x + 4 ≥0
(x − 2)2 ≥0 x∊R