geometria KASIA: Proszę o pomoc w zadaniu: W trójkącie ABC dane są: kąt ACB = 120 stopni, |AC| = 6, |BC|= 3 . Dwusieczna kąta ACB przecina bok AB w punkcie D. a) oblicz długość odcina CD b) jaki jest związek między długościami promieni: okręgu opisanego na trójkącie ADC i okręgu opisanego na trójkącie DBC ? Odpowiedź uzasadnij.

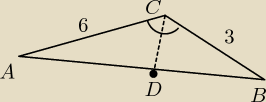
Wojteq66: a) Możesz obliczyć ze wzoru na pole trójkąta

	1
PABC=		* ab * sinx = 9* sin(120)= 9*sin(180−60)=9*sin60
	2

kąt ACD = kąt DCB = 60 stopni P_ABC = P_ADC + P_DBC

	1		1
9*sin60=		*6xsin60 +		*3xsin60 // sin60
	2		2

9= 4.5x //4.5 x=2

KASIA: ahaa już wiem dziękuję a podpunkt b?

Wojteq66: tego narazie nie moge wykminić

KASIA: ok ja też jeszcze spróbuję coś pomyślec

Wojteq66: podziel się rozwiązaniem jak wpadniesz na trop

KASIA: chyba już wiem.

KASIA: obliczyłam długości boków AD i DB z tw. cosinusów: |AD| = √28 i |DB| = √7 nastepnie dla trojkąta ADC z pola: ¹₂*6*2* sin 60 = ^6*2*√28_4R stąd R= √²⁸₃ dla trójkąta DBC ¹₂*2*3*sin 60 = ^3*2*√7_4R stąd R = √⁷₃ i obliczyłam stosunek . wyszło 2

Kamil Turkiewicz: R można jeszcze z tw sinusów ale to dowolne bo i tak trzeba obliczyć AD i BD i wychodzi na to samo