... Tes: OMG 1.W trójkącie prostokątnym poprowadzono dwusieczną kąta prostego. Oblicz kąty ostre tego trójkąta, wiedząc że środek okręgu wpisanego dzieli odcinek dwusiecznej w stosunku √3 : √2 licząc od wierzchołka kąta prostego. 2. Wysokość CC1 poprowadzona z wierzchołka kąta prostego trójkąta prostokątnego ABC jest równa 4 i dzieli bok AB na dwie częśći AC1 i C1B takie że AC1 : C1B = 1:8. Oblicz długość odcinka równoległego do wysokości CC1, dzielącego pole trójkąta ABC na połowy. 3. Dany jest okrąg o promieniu r. Przez dowolny punkt M tego okręgu poprowadzono styczną, na której obrano punkty A i B, leżące po przeciwnych stronach punktu M, takie że AM = MB = a. Oblicz długość promienia okręgu przechodzącego przez punkty A i Bstycznego do danego okręgu. W 3 prosiłbym o rysunek, sam nie wiem jak to w ogóle narysować.

Tes: up

Tes: up

KM: To są zadania z OMG?

Tes: Czyli nie wiesz jak zrobić?

Tes: wie ktoś może jak ruszyć którekolwiek z zadań? =(

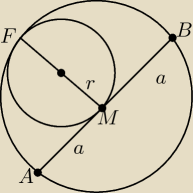
Wojteq66: coś takiego bym rysował, tylko ze nie moge obrac sobie konkretnych punktów... ale działałbym w kierunku okręgu opisanego na trójkącie może.. jakby dorysować krawędź AF i BF to masz trójkąt gdzie wysokośc jest 2r małego okręgu. tylko co to da.. bo AB to tylko cięciwa...

Tes: No właśnie, próbuje z różnymi wielkościami okręgów ale nic nie mogę wskórać. Przy długości odcina AB < średnicy okręgu, mniejszy okrąg jest wpisany w trójkąt ABF...i nic poza tym

Tes: Ktoś wspomoże?

Godzio: Co do pierwszego kąty mają mieć miary typu 30^o czy może 42 np ?

Wojteq66: a masz odpowiedzi do tego ?

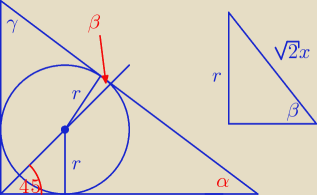
Godzio: r√2 = √3x

	√6
r =		x
	3

180 − β = 180 − 45 − α ⇒ β = 45 + α

r		√2
	= sinβ =		(sinα + cosα)
√2x		2

r		√6
	= sinα + cosα ⇒ sinα + cosα =
x		3

	√6
cosα =		− sinα
	3

	2		2√6
1 − sin2α =		−		sinα + sin2α
	3		3

	2√6		1
2sin2α −		sinα −
	3		3

6sin²α − 2√6sinα − 1 Δ = 24 + 24 = 48 √Δ = 4√3

	2√6 + 4√3		√6 + 2√3
sinα =		=		≈ 0,985 ⇒ α ≈ 80o, γ = 10o
	12		6

	√6 − 2√3
sinα =		< 0
	6

No zobaczymy czy dobrze

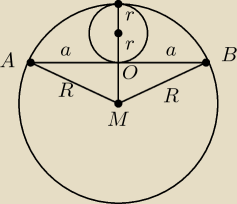
Kuba131: (OM)² + a²= R² R= OM + 2r Po przekształceniach R= 2r + √R²−a² R − 2r = √R²−a² Podnosząc stronami do kwadratu R² − 4Rr + 4r² = R² − a² Przezucając przekształcając otrzymujemy R = (a² + 4r²)/r

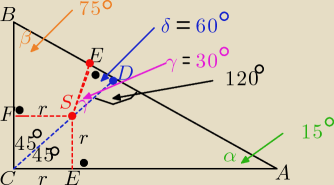
Eta: |CS| = x√3 , |DS|= x√2 , x >0 ICS| = r√2 , to r√2= x√3

	x√3
więc r=
	√2

z trójkata prostokatnego DES mamy;

	r		x√3   √2		√3
cosγ=		=		=
	IDS|		x√2		2

zatem γ= 30^o to: |<SDE|= 60^o => |<ADC|= 120^o więc α= 180^o −(45^o+120^o) = 15^o to β= 90^o −15^o = 75^o