pole rombu PILNE!!: W rombie o polu 4,80dm poprowadzono odcinek długości 2,4dm, który łączy środki sąsiednich boków rombu przy kącie rozwartym. Oblicz: a) długość przekątnych rombu b) obwód rombu c) wysokość rombu d) pole trójkąta wyciętego z rombu przez dany odcinek

PILNE!!: wrrrrrr..

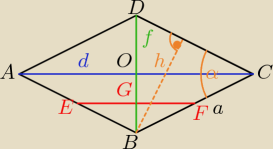
dero2005: |EF| = 2,4 dm

CO		CB
	=		podobieństwo trójkątów
FG		CF

CB = a CF = ^a₂ FG = 1,2 CO = 2FG = 2,4 CO = ^d₂ d = 2*CO = 4,8 d = 4,8 dm − przekątna dłuższa P = ¹₂df = 4,8 pole rombu f = 2 dm − przekątna krótsza (^f₂)² + (^d₂)² = a² tw Pitagorasa a = 2,6 dm − bok O = 4a = 4*2,6 = 10,4 O = 10,4 dm − obwód P = a²*sinα pole rombu

	P
sinα =
	a2

h
	= sinα
a

	P		4,8
h = a*sinα =		=		= 1,85 dm − wysokość
	a		2,6

pole trójkąta

	FE*GB
P =		gdzie FE = 2,4 GB = f4 = 0,5
	2

P = 0,6 dm²

cxv: β∑≥ππππππ

jack:

Masny ben : j=60