planimetria Dawid: W czworokacie ABCD wpisanym w okrag dlugosci lukow odpowiadajacym cieciwa AB,BC i CD sa rowne. Wykaz ze czworokat ABCD jest trapezem. moze ktos pomoc?

ceaser I: https://matematykaszkolna.pl/strona/872.html

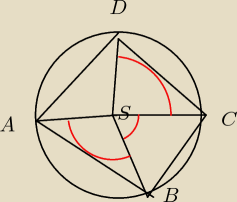
ICSP: Powiedzmy ze jest wpisany. Czerwone kąty są takie same to chyba oczywiste. Powstają trójkaty równoramienne. kąt ABC = kątowi DCB. Teraz z warunku wpisania c w okrąg. kąt ADC = 180−kąt CBA kąt DAB = 180 − kąt DCA z tego wynika że kąt DAB = kątowi ADC oraz kąt DCB = kątowi ABC co kończy dowód

ICSP: DAB = 180 − kąt DCB oczywiście mój błąd.

Dawid: ok dzieki wielkie

andrzej: a ja mam pytanie do tego zadania, jezeli wiemy ze te luki sa rowne to tez dlugsci bokow sa rowne? a jezeli trzy sa rowne to 4 tez jest rowny? i wtedy mamy ze sa rownolegle a trapez jest gdy ma co najmniej 1 pare bokow rownoleglych?

Artur_z_miasta_Neptuna: trzy równe nie oznacza, ze i czwarty taki sam niech te trzy kąty mają miarę powiedzmy 100^o ... wtedy czwarty musi miec miare 60^o i się posypalo wszystko

andrzej: a no tak w sumie tak dzieki