Prosiłabym o pomoc w wyliczeniu tego zadania
kasia: Długości boków równoległoboku wynoszą 1 i √3, a kąt przy wierzchołku B ma miarę 150 stopni.
Oblicz promień okręgu opisanego na trójkącie ABD.
3 kwi 14:18
ceaser I: podziel równoległobok na pół i powstanie przekątna AC, wylicz jej odległość za pomocą
twierdzenia cosinusów a następnie. R oblicz za pomocą twierdzenia sinusów

3 kwi 14:46
kasia: ok dzięki

3 kwi 15:01
kasia: chyba jednak nie dam rady

moglbys mi to rozpisac?
3 kwi 15:11
ceaser I:
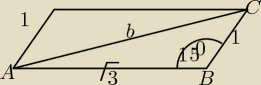
3 kwi 15:27
ceaser I: b2=√32+12−2*√3*1*cos150
3 kwi 15:28
ceaser I: cos 150= 180−150= cos30,cos w II ćwiartce jest ujemny wiec mamy −cos30
3 kwi 15:28
ceaser I: b=√7
3 kwi 15:30
ceaser I: z tw sinusow:
b/sin150=2R
3 kwi 15:31
ceaser I: sin150=sin30=1/2
podstawiasz i R wychodzi √7
tak jest w odpowiedziach ?
3 kwi 15:33
dero2005:
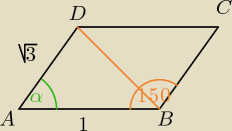
Suma miar kątów sąsiednich w równoległoboku wynosi 180
o
α = 180 − 150 = 30
o
tw cosinusów
|DB|
2 = 1
2 + (
√3)
2 − 2*1*
√3*cos30
o = 1 + 3 − 3 =1
|DB| = 1
tw sinusów
R = 1
3 kwi 15:43
ceaser I: @dero2005, ale cos150 jest w II ćwiartce więc cos jest ujemny
3 kwi 15:45
dero2005:
do czego potrzebny cos 150o?
3 kwi 15:47
kasia: fajnie dzięki

3 kwi 16:02
ceaser I: kasia a jaki jest wynik w odp ?
3 kwi 16:05
kasia: nie mam do tego odpowiedzi

3 kwi 16:08


 moglbys mi to rozpisac?
moglbys mi to rozpisac?

 Suma miar kątów sąsiednich w równoległoboku wynosi 180o
α = 180 − 150 = 30o
tw cosinusów
|DB|2 = 12 + (√3)2 − 2*1*√3*cos30o = 1 + 3 − 3 =1
|DB| = 1
tw sinusów
Suma miar kątów sąsiednich w równoległoboku wynosi 180o
α = 180 − 150 = 30o
tw cosinusów
|DB|2 = 12 + (√3)2 − 2*1*√3*cos30o = 1 + 3 − 3 =1
|DB| = 1
tw sinusów

