planimetria
skazany na zyciowa porazke:
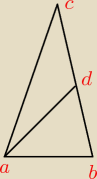
Punkt D leży na boku BC trójkata rownoramiennego ABC, w którym AC=BC. Odcinek AD dzieli trójkat
ABC na dwa trójkaty rownoramienne w taki sposob, ze AD=AC oraz AB=BD. Udowodnij ze ∡ADC=5*∡ACD
2 kwi 23:14
rączszka: Czemu masz taki sadystyczny nick
2 kwi 23:17
skazany na zyciowa porazke: A Ty po co zadajesz tak beznadziejne pytania? teraz juz nikt mi nie pomaze bo jest jedna odp na
pyt i nikt tu nie wejdzie:(
2 kwi 23:24
kox: mature zdajesz w tym roku ?
2 kwi 23:25
skazany na zyciowa porazke: tak
2 kwi 23:25
Eta:
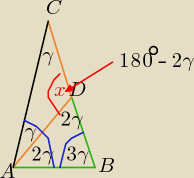
x = |<ADC| = 180
o −2γ
suma miar kątów trójkącie ABC
mamy: 3γ+3γ+γ= 180
o => 7γ= 180
o
to:
x= 180
o −2γ = 7γ −2γ=
5γ
zatem: |<ADC| = 5* |< ACD|
co kończy dowód.
P.S. Głowa do góry, dasz radę .... nie łam się,
Powodzenia::
3 kwi 00:19