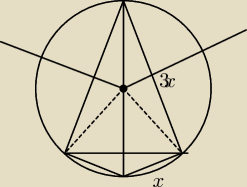
HARD Tes: Rys zrobiłem do 1, jakoś podobieństwo chyba muszę wykorzystać: 1. W okręgu wpisano dwa trójkąty równonamienne o wspólnej podstawie. Stosunek długości ramion tych trójkątów wynoi 1:3. Oblicz stosunek długości wysokości opuszczonych na wspólny bok. 2. W trójkącie prostokątnym poprowadzono dwusieczną kąta prostego. Oblicz kąty ostre tego trójkąta, wiedząc że środek okręgu wpisanego dzieli odcinek dwusiecznej w stosunku √3 : √2 licząc od wierzchołka kąta prostego.

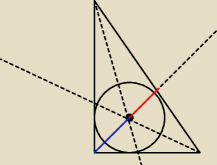
Tes: niebieska − √3x czerwona − √2x

Tes: Rys wyżej do zad 2, nasuwa się twierdzenie o dwusiecznej. Prosiłbym o pomoc

Tes: up

Tes: up

Tes: ...

Tes: nikt nie wie jak to zrobić?

ICSP: Eta pierwsze 9:1?

Godzio:

	1		ah
P1 =		x2sinα =
	2		2

	9		ah1
P2 =		x2sinα =		( sin(180 − α) = sinα, skorzystałem z warunku
	2		2

wpisania czworokąta w okrąg) Dziele oba równania:

1   x2sinα   2		ah   2
	=
9   x2sinα 2		ah1   2

1		h
	=
9		h1

Eta:

Tes: Rozwiązałem 1, ale dzięki za pomoc. 2 nie mogę zmęczyć =/