W trójkącie równoramiennym ABC Bart: 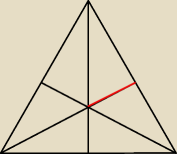W trójkącie równoramiennym ABC ac=bc podstawa ab = 8√5 = cf, gdzie cf jest wysokością poprowadzoną z wierzchołka C. Oblicz odległość punktu przecięcia wysokości tego trójkąta od jego ramion.

ukasz: Polecam podpisać na rysunku. . . bo brak oznaczeń i nie wiadomo o co chodzi

Bart: rysunek wynika z treści, chciałem pokazać tylko jak mają się przecinać wysokości. Mam obliczyć długość tej czerwonej linii. Prosiłbym o pomoc z tym zadaniem.

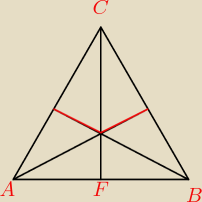
Bart: ABCF

kamis: |AD| − wysokość opuszczona na ramię |BC|

	1
Pole =		* 8√5 * 8√5 = 160
	2

Długość ramienia − √(8√5)² + (4√5)² = 20 Długość wysokości opuszczonej na ramię − 16 Długość odcinka DC = 20² − 16² = 12 Z podobieństwa trójkątów:

8√5		4√5
	=
4		x

16√5 = 8x√5 x = 2

kamis: Mały błąd się wkradł:

8√5		4√5
	=
12		x

48√5 = 8x√5 x = 6

Tes: Dzięki wielkie, a mógłbyś powiedzieć skąd to się wzięło: Długość odcinka DC = 20² − 16² = 12 ?

kamis: Z trójkąta ADC i twierdzenia Pitagorasa