wyznacz wzór a_n Koli: Wyznacz ogólny wyraz ciągu (a_n), jeśli suma n początkowych jego wyrazów wyraża się wzorem S_n=3n²+4n

morfepl: S_n−1=3(n−1)²+4(n−1)=3n²−6n+3+4n−4=3n²−2n−1 S_n−S_n−1=a_n a_n=3n²+4n−(3n²−2n−1)=6n+1 jak coś popitoliłem to niech mnie ktoś poprawi

Trivial: Suma jest rzędu n², więc być może ciąg a_n jest ciągiem arytmetycznym. Obliczamy a₁ (wystarczy że policzymy sumę pierwszego składnika). a₁ = S₁ = 3+4 = 7. a₁ + a₂ = S₂ = 3*4 + 4*2 = 12 + 8 = 20 a₂ = 20 − 7 = 13. r = 13 − 7 = 6. a_n = 7 + 6*(n−1) = 7 + 6n − 6 = 6n + 1 Sprawdzamy:

	7 + 6n + 1
Sn =		n = (3n + 4)n = 3n2 + 4n OK.
	2

Trivial: Zapomniałem o tej prostej własności.

Koli: no kurde moze mi ktos dac link gdzie sa wypisane wszystkie wlasnosci ciagow ? a przynajmniej te najpopularniejsze

dazy: wzór ogólny ciągu: a_n=a₁+(n−1)r do wzoru Sn podstawiamy n=1, dzięki temu otrzymamy sumę pierwszego wyrazu, a jednoczeście pierwszy wyraz ciągu a₁ S₁= 3*1² + 4*1=7 Teraz obliczamy S_n dla n=2 S₂= 3*2² + 4*2=20 Obliczamy drugi wyraz ciągu a₂ a₂= S₂ − S₁ = 20−7=13 Obliczam r r=a₂ − a₁ = 13−7=6 Podstawiam do wzoru ogólnego ciągu: a_n=a₁+(n−1)r a_n=7+(n−1)6 a_n=7 + 6n − 6 a_n=6n +1 Odp. a_n=6n +1

Koli: no kurde moze mi ktos dac link gdzie sa wypisane wszystkie wlasnosci ciagow ? a przynajmniej te najpopularniejsze

Nattik: @dazy, dlaczego S1=a1?

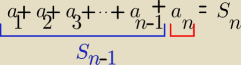
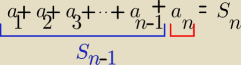ekierka: To a_n= S_n−S_n−1