mam takie zadanie trójkącie prostokątnym cosinus tangens

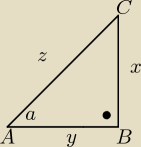
trygonometria matura: rysunek

Mam takie zadanie: W trójkącie prostokątnym ABC cosinus i tangens kąta przy wierzchołku A są równe. Oblicz sinus tego kąta. Moja pierwsza myśl to: tgx = cosx

sinx
	= cosx / *cosx
cosx

sinx = cos²x sinx = 1 − sin²x sin²x + sin − 1 = 0 Dobrze to zacząłem ? Oczywiście zamiast x to powinno być α

2 kwi 11:12

matura: Góra

2 kwi 11:14

Bizon: ... pewnie emotka

2 kwi 11:16

matura: To ciągniemy dalej: t = sinx, t∊<−1,1> t² + t − 1 = 0 Δ = 1 + 4 = 5 √Δ = √5

	−1 − √5
t₁ =
	2

	−1 + √5
t₂ =
	2

Jakiś pomysł co dalej emotka

2 kwi 11:18

ICSP: t₁ <−1 dlatego jest sprzeczne.

	−1 + √5
sinx =		.
	2

2 kwi 11:19

morfepl: trzeba jedno t wywalić, gdyż jest <0

2 kwi 11:20

matura: W sumie to chyba tylko oszacować: √5 ≈ 2,24

	−1 − 2,24		−3,34
t₁ =		=		∊ <−1,1>
	2		2

	−1 + 2,24		1,24
t₂ =		=		∊ <−1,1>
	2		2

Czyli rozwiązanie to:

	−1 − √5		−1 + √5
sinx =		v sinx =
	2		2

tak?

2 kwi 11:20

matura: Poprawka: t₂ odpada

2 kwi 11:21

matura: Co ja pisze: t₁ nie pasuje emotka

sorki i dziękuje pięknie emotka

2 kwi 11:22

morfepl: a czemu t₂ odpada, przecież jest dobrze, to t₁ jest sprzeczne nie tylko z funkcjami trygonometrycznymi, ale także z założeniami zadania, że α∊(0;π/2)

2 kwi 11:23