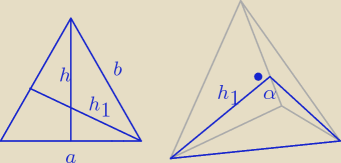dwuscienny kat meg: Wysokość ostrosłupa prawidłowego czworokątnego jest dwa razy krótsza od krawędzi podstawy tego ostrosłupa. Wyznacz miarę kąta: dwuściennego pomiędzy dwiema sąsiednimi ścianami bocznymi tego ostrosłupa.

Godzio : H − wysokość ostrosłupa a = 2H −− krawędź podstawy b − krawędź boczna h,h₁ − wysokości ściany bocznej

	1		a√3
h2 = (		*		)2 + H2
	3		2

	a2
h2 =		+ H2
	12

	H2
h2 =		+ H2
	3

	4
h2 =		H2
	3

	2
h =		H
	√3

	2		a√3
b2 = H2 + (		*		)2
	3		2

	a2
b2 = H2 +
	3

	4
b2 =		H2
	3

	2
b =		H
	√3

	ha		bh1		2		1
P =		=		→		H * H =		H * h1
	2		2		√3		√3

2H = h₁ Z tw. cos: h₁² + h₁² − 2h₁²cosα = a² 8H² − 8H²cosα = 4H² −8cosα = −4

	1
cosα =		⇒ α = 30o
	2

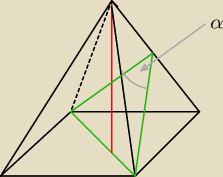meg: dziwne, w odpowiedzi jest 120.. i nie bardzo rozumiem ten rysunek Twój a czy ja dobrze to narysowałam?znaczy niby to jest kąt pomiędzy ścianami bocznymi, ale nie wiem czy sobie taki trojkat zielony moge zrobic?

meg: Nie no to napewno jest źle co narysowałam ale nie potrafie tego wyobrazic:(

Godzio : Dobrze narysowałaś ... Ja zrobiłem zadanie dla ostrosłupa prawidłowego Trójkątnego

Godzio : Jeśli nikt nie pomoże to czas będę mieć około 22, albo jeszcze wyhacze coś w czasie dnia i pomogę

meg: No właśnie tak mi się wydawało, że to dla trójkątnego ale pomyslalam ze moja wyobraznia szwankuje i tam gdzes jest rzeczywiscie czworokat na rysunku Byłabym bardzo wdzieczna za pomoc no chyba ze jakos sama na to wpadne

Godzio: Dobra mam 30 min Pisać rozwiązanie ?

Godzio:

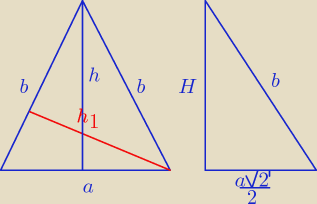
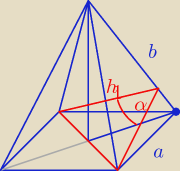Godzio: a = 2H

	a√2
H2 + (		)2 = b2
	2

H² + (H√2)² = b² ⇒ H² + 2H² = b² ⇒ b² = 3H² ⇒ b = √3H

	1
h2 + (		a)2 = b2
	2

h² = 3H² − H² h = √2H

	b * h1		ah		2√2H
Pściany bocznej =		=		⇒ √3Hh1 = 2√2H2 ⇒ h1 =
	2		2		√3

Z tw. cosinusów: h₁² + h₁² − 2h₁²cosα = (a√2)²

	8H2		8H2
2 *		− 2 *		cosα = (2H√2)2
	3		3

16H2		16H2
	−		cosα = 8H2 /: 8H2
3		3

2		2
	−		cosα = 1
3		3

	2		1
−		cosα =
	3		3

	1
cosα = −		⇒ α = 120o
	2

meg: Dziękuję Godzio ! Czy istnieją zadania któych nie dałbyś rady zrobić?

Godzio: Oj i to ile

Gal anonim: Bardziej na około się nie dało