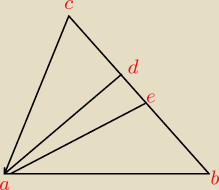
Na boku BC (BC>AC) trojkąta ABC wybrano punkt D tak, by ∡CAD=∡ABC. Odcinek AE jest dwusieczną
kąta DAB. Udowodnij, że AC=CE
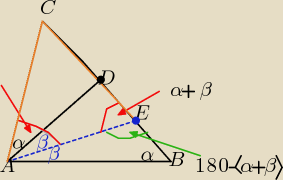Myślę ,że już jasne 
Przeprowadź dowód, zapisz odpowiednio miary kątów, które zaznaczyłam
i otrzymasz tezę:
ΔAEC jest równoramienny , o ramionach AC i EC => |AC|= |EC|