Udowodnij nierówność

Udowodnij nierówność pablo: Udowodnij nierówność: x / (1+ x) < ln (1 + x ) < x dla x> 0.

2 kwi 00:26

Eta:

	x
f(x) =		, g(x)= ln(x+1) , h(x)= x i x>0
	x+1

	1
f^'(x)=
	(x+1)²

	1
g⁽x)=
	1+x

h^'(x)=1 i x>0

1		1
	<		< 1 −−−−− zachodzi
(1+x)²		x+1

Co Godzio na to ? emotka

2 kwi 01:03

Godzio: A Godzio na to jak na lato emotka

2 kwi 01:04

Eta:

2 kwi 01:05

Eta: Można też skorzystać z wykresów tych trzech funkcji Godzio ........ namaluj je ładnie emotka

2 kwi 01:15

Godzio: Trochę to potrwa

2 kwi 01:22

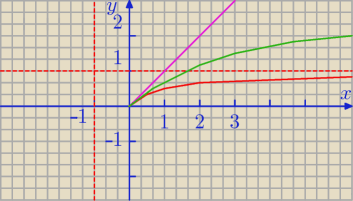
Godzio: rysunek

x > 0

	x		1
f(x) =		= −		+ 1
	x + 1		x + 1

g(x) = ln(1 + x) h(x) = x

2 kwi 01:34

Eta: Ślicznie emotka

2 kwi 01:39

Ajtek: Cześć Godzio, miałeś wątek odnośnie swojej przyszłości o ile mnie pamęć nie myli. Byłem trozkę spóźniony, o jakies 20 godz., ale też tam coś wpisałem. Przeczytałeś?

2 kwi 01:42

Godzio: Właśnie przeczytałem emotka

2 kwi 01:45

Ajtek: I co

2 kwi 02:04