Wyjątkowo poirytowany:
Stereo− kur** −metria . Szlag.
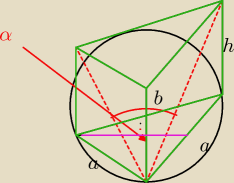
Podstawą graniastosłupa jest trójkąt prostokątny równoramienny wpisany w okrąg o promieniu r.
Kąt między przekątnymi ścian bocznych wychodzącymi z tego samego wierzchołka podstawy jest
równy α. Wyznacz objetość graniastosłupa.
Rysunek robilem sam. nie gwarantuje ze jest dobrze.
1 kwi 20:51
Ajtek: Wskazówka:
Jeżeli Δ prostokątny jest wpisany w koło, to przeciwprostokątna jest jego średnicą.
1 kwi 21:00
Wyjątkowo poirytowany: zaraz zobaczę...
1 kwi 21:04
Wyjątkowo poirytowany: nie wiem...
1 kwi 21:13
Wyjątkowo poirytowany:
1 kwi 21:51
Wyjątkowo poirytowany:
1 kwi 22:03
Wyjątkowo poirytowany: Policzy to ktoś ?
1 kwi 22:15
Mila:
niestety nie czuje tych katów ,gdy musiałąm robic zadanie to wycinałam z ziemniaka bryły ,zeby
zobaczyć jak to wyglada
Srednica =b=2r
a2+a2=(2r)2
2a2=4r2
a=√2r
1 kwi 22:48
kto: ktos to zrobi?
1 kwi 23:32
anybodyhere?: odswiezam
1 kwi 23:45
anybodyhere?: ref
2 kwi 00:15
Eta:
Napisz porządnie treść zadania
O który kąt chodzi?
o kąt między przekątnymi wychodzacymi z wierzcołka
ścian prostopadłych ?
czy z wierzchołka ścian , które nie są prostopadłe ?
bo to jest ważne
2 kwi 00:32
Ajtek: Wiesz
Eta, być może i taka jest treść tego zadania, tylko brakuje jakiejs części, np.
rozpatrz dwa przypadki
. Zgodzisz się ze mną?
2 kwi 01:21
Eta:
Oczywiście
........ wtedy trzeba rozpatrzyć obydwa przypadki.
Dlatego pytałam o treść .
2 kwi 01:30
Ajtek: Moją pierwszą podpowiedź uzależniłem od rysunku (głównie) dopasowując do niego treść.
Jaki z tego wniosek wyciągnąłem
Nigdy nie ufaj oczętom, nawet swoim
.
2 kwi 01:34
Eta:
He he ... a
poirytowany napisał:
"rysunek robiłem sam, nie gwarantuję,że jest dobrze"
2 kwi 01:43
Ajtek: Eta do tego zmierzałem.
Natomiast ta druga wersja troszkę by utrudniła sprawę
. Tzn. przekątne ścian nie będących
prostopadłymi.
2 kwi 01:47
Eta:
2 wersja) ze wzoru cosinusów i też wyjdzie
2 kwi 01:55
Godzio :
Pora spać
2 kwi 01:58
Ajtek: To fakt,
natomiast po chwili zastanowienia doszedłem jednak do wniosku, być może mylnego, iż ta tresć z
ten rysunek są poprawne.
Kąt α zapisujemy jako 2β i później śmigamy z Δ równoramiennego. Wyliczmy przekątną sciany
bocznej z trygonometrii, następnie dł. przyprostokatnej z Pitagorasa a później juz łatwo
obliczyć objetość
. To tak czysto teroretycznie bez rozpisywania.
2 kwi 02:02