Obwód trójkąta Louis: Oblicz obwód trójkąta ABC o wierzchołkach A=(1,5) B=(−3,−3) C=(−2,4).

dero2005: d = √(x₂−x₁)²+(y₂−y₁)² |AB| = √(−3−1)²+(−3−5)² = √−4²+(−8)² = √16+64 = √80 = 4√5 |BC| = √(−2+3)²+(4+3)² = √1²+7² = √1+49 = √50 = 5√2 |CA| = √(1+2)²+(5−4)² = √3²+1² = √9+1 = √10 O = |AB| + |BC| + |CA| = 4√5 + 5√2 + √10

Gustlik: Dero, czemu nie pokażesz wektorami? Ta sama metoda, a bardziej przejrzysta. Liczysz współrzędne wektorów zawierających boki trójkąta, a potem podstawiasz do tw. Pitagorasa, np. AB^→=[−3−1, −3−5]=[−4, −8] |AB|=√(−4)²+(−8)²=√16+64=√80=4√5 Tasiemcowe wzory nie są przejrzyste, a obliczanie współrzednych wektorów jest proste jak konstrukcja młotka, potem wzór na długość wektotra |w^→|=√w_x²+w_y² i po sprawie.

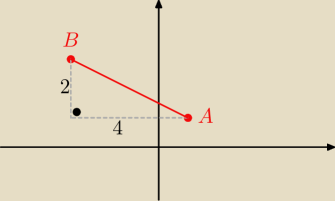
Eta: wystarczy policzyć "kratki"( o ile punkty są kratowe) i z tw. Pitagorasa |AB|²= 4²+2² =>|AB|= √20= 2√5

Gustlik: W przypadku liczb całkowitych tak, ale najbardziej przejrzysty i prosty jest sposób za pomocą wektorów. Naprawdę polecam kazdemu nauczyć się wektorów, mimo iz na podstawie nie są one NIESTETY wymagane, a baaaardzo ułatwiają życie w zadaniach z geometrii analitycznej, choćby przy obliczaniu pól figur − można ominąć wtedy żmudne obliczanie odcinków, boków, wysokości itp. Wektory to podstawa geometrii analitycznej i tu znowu muszę zwyzywać od debili tego, kto je usunął z podstaw.