Zbiór nierówności tiesto17: Pomóżcie obliczyć zbiór liczb tej nierówności, bo kompletnie nie czaje: x−3≥2

tiesto17: x−3≥2 wytłumaczę ci to po chłopsku, ja robię to tak 1) przepisuje to samo, ale z przodu stawiam identyczny znak (skierowany w tą samą stronę) a przed nim stawiam liczbę dwa tyle że z minusem (bo musi być odwrotność liczby): −2≥x−3≥2 2) Teraz trzeba to sprowadzić do takiej postaci by w środku pozostał sam x A więc by z x−3 zrobić x to trzeba do wyrażenia x−3 dodać 3 wtedy dostaniemy samo x, lecz trzeba też dodać to 3 do każdego wyrażenia znajdującego się między znakami, można powiedzieć że obustronnie dodajemy 3: −2≥x−3≥2 I+3 3−2≥x−3+3≥2+3 1≥x≥5 3) z wyrażenia 1≥x≥5 uzyskujemy dwa punkty: 1≥x oraz x≥5 czyli x≤1 (po prostu ustawiłem x po lewej stronie, wyrażenie jest takie same nadal) oraz x≥5 4) Teraz musimy to zaznaczyć na osi: rysunek 1 5) oraz zaznaczamy zakresy liczb 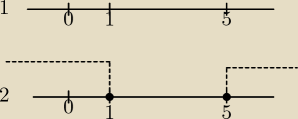x≤1 oznacza wszystkie liczby mniejsze od 1 a x≥5 wszystkie liczby większe od 5 (z włączeniem piątki bo mamy znak większe lub równe, tak samo jest z liczbą jeden) − rysunek 2 Potem wystarczy zapisać zbiór liczb tej nierówności czyli: xε=(−∞,1>∪<5,+∞) I to jest koniec zadania Troszkę długie ale mam nadzieje że zrozumiale opisane

tiesto17: Nie wiem czemu odpisujesz pod moim nickiem, ale nic nie szkodzi, najwazniejsze że wreszcie to pojąłem, tyle czasu się z tym w szkole męcze, różnych nauczycieli od matmy miałem, ale żaden nie potrafił tak tego wytłumaczyć bym pojął to raz na zawsze, dopiero tobie się to udało, dodam że teraz wydaje się to całkowicie banalne, wziąłem sobie inny przykład i zrobiłem go raz dwa, Dzięki wielkie koleś, kimkolwiek jesteś ps. szybko ci to poszło, opisanie tego ale ogólnie widze że tempo rozwiązywania zadań na tej stronce jest kosmiczne