analityczna ICSP: Zaciekawiła mnie jedna sprawa i mam z tym związany pewien problem: Zadanie(wersja srkócona bez zbędnego spamu) Kwadrat o przeciwległych wierzchołkach A(1;3) ; C(7;1).Wyznaczyć pozostałe dwa wierzchołki Zadanie potrafie rozwiazać ale zastanawiałem się nad jedną rzeczą: prosta ac:

	1		1
y = −		x + 3
	3		3

środek kwadratu: (4;2) prosta bd" y = 3x − 10 I teraz pojawia się problem. Wpadłem na pomysł że gdyby zakręcić prostą ac o 45^o otrzymam prostą ab lub ad. Wtedy z układu równań tej prostej oraz prostej bd mógłbym obliczyć odpowiednio wierzchołki. Nie wiem tylko jak wyznaczyć współczynnik kierunkowy tych dwóch prostych bo wiem że będą przechodziły przez punkt A. Pozdrawiam.

ICSP: up.

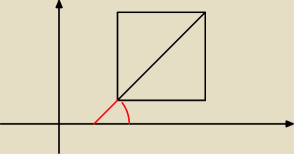
uhu: Probowałeś coś z tym tgα kombinować ?

ICSP: problem w tym że kwadrat jest troszkę "krzywo" i

uhu: Nie lepiej wektorami ?

ICSP: Nie za bardzo lubię wektory. Za to uwielbiam układy równań i dlatego wszystko próbuję do nich dopasować.

ICSP: Dlatego gdybym miał równanie prostej ab i symetralnej odcinka ac bez problemu wyznaczyłbym wierzchołek B

uhu: Jeśli żadna przekątna nie jest równoległa do osi x to ją przecina wiec tgα dalej można obliczyć

ICSP: dobrze więc mamy: prosta ac jest przekątną.

	1
jesj współczynnik kirunkowy to −
	3

ze wzoru:

	1
tgα = −		nie za bardzo rozumiem co mi to daje.
	3

miro0r: Wyznacz sobie prosta AC i długość odcinka |AC|. |AC|=a√2 wyliczasz a i masz długość |AB|. potem do wzoru na długość |AB| za "y" wstawiasz prostą AC i przyrównujesz do "a" i masz już punkt B a potem sobie poradzisz

uhu: Wprowadziłem cie w błąd bo tg90 nie istnieje, myślałem że tg90=1 wtedy y=−x+b i wstawiasz A ale nic z tego, jednak może jakoś się to da wykombinować tym sposobem

Eta: Witam Proponuję tak: rozwiąż układ równań prostej zawierającą przekątną BD

	1
i okręgu o środku S i promieniu r=		|AC|
	2

Otrzymasz jednocześnie współrzędne obydwu punktów B i D

ICSP: Witam Eto tak właśnie zrobiłem. Tylko chcę się dowiedzieć czy istnieje możliwość wyznaczenia wzorów prostych ab i ad bo wtedy to już będzie na prawdę z górki:

Zimny: Po co sie meczyc. Wyznaczasz srodek AC, prosta AC, szukasz prostopadlej do AC przechdozacej przez punkt S(srodek AC) i opisujesz okrag o promieniu SC i uklad rownan z prosta BD. Duzo latwiej i szybciej na wektorach.

think: ICSP współczynnik kierunkowy to tgα

	1
tgα = −
	3

	1
teraz z tablic musisz odczytać dla jakiego kąta tg przyjmuje wartość −		do tego kąta
	3

dodajesz 45 stopni i szukasz wartości tg(α + 45) , to będzie współczynnik kierunkowy prostej zawierającej bok ale jak inni wspominają ta zabawa to skórka nie warta wyprawki, jeśli nie wychodzi z tego okrągły kąt, bo będziesz miał błąd przybliżenia.

ICSP:

	1
Problem w tym że nie umiem odczytać dla jakiego kata tg przyjmuje wartość −		. Jednak już
	3

znalazłem sposób na wyznaczenie tych dwóch prostych. Dziękuję wszystkim za pomoc.

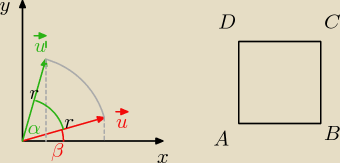
Trivial: Wyprowadzimy wzór na obrót wektora o kąt α. u = (u_x, u_y) Ale możemy zapisać to inaczej, wykorzystując długość wektora u, czyli r. u = (u_x, u_y) = (rcosβ, rsinβ) Teraz, wektor u' zapisujemy w formie u' = (rcos(β+α), rsin(β+α)) = (rcosβ⋅cosα − rsinβ⋅sinα, rsinβ⋅cosα + rcosβ⋅sinα) = = (u_x⋅cosα − u_y⋅sinα, u_y⋅cosα + u_x⋅sinα) = (u_xcosα − u_ysinα, u_xsinα + u_ycosα), co można również zapisać w formie macierzowej

	cosα sinα −sinα cosα
u' = u⋅		.

Odnośnie zadania, to można rozwiązać je w taki sposób: 1. Wyznaczamy wektor AC. 2. Obracamy go o kąt 45^o zgodnie ze wzorem i otrzymujemy wektor [P[AC]']. 3. Aby otrzymać punkt D przesuwamy punkt A o wektor ¹∕_√2⋅AC'. 4. Aby otrzymać punkt B przesuwamy punkt C o wektor −¹∕_√2⋅AC'. A = (1, 3) C = (7, 1) 1. AC = (7−1, 1−3) = (6, −2).

	√2		√2		√2		√2
2. AC' = (6⋅		− (−2)⋅		, 6⋅		− 2⋅		) = √2⋅(4, 2).
	2		2		2		2

3. D = A + (4, 2) = (5, 5). 4. B = C − (4, 2) = (3, −1).

dero2005: prosta AC y = −¹₃x+¹⁰₃ a_A = −¹₃ szukamy współczynników kierunkowych prostych AB i AD (skręcamy prostą AC o 45^o)

	a1−a2
tgφ = |		| tg 45o = 1 a1 = −13
	1+a1*a2

a−1−a2		a1−a2
	= 1 lub −		= 1
1+a1*a2		1+a1*a2

a₂ = −2 lub a₂ = ¹₂ szukamy prostych o współczynnikach ¹₂ i −2 i przechodzących przez punkt A(1,3) y_AD = −2(x−1)+3 y_AB = ¹₂(x−1)+3 y_AD = −2x + 5 y_AB = ¹₂x +⁵₂ porównujemy proste AD i BD i znajdujemy punkt D 3x−10 = −2x+5 x = 3 y = −1 D(3,−1) porównujemy proste AB i BD i znajdujemy punkt B ¹₂x + ⁵₂ = 3x − 10 x = 5 y = 5 B(5,5)

ICSP: Dziękuję wam jeszcze raz Właśnie o to mi chodziło