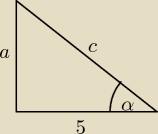
| a | 1 | |||
sinα= | = | |||
| c | 3 |
| a | 1 | ||
= | |||
| c | 3 |

 dane
b = 5
sinα = 13
sin2α + cos2α = 1
cos2α = 1 − sin2α
cos2α = 1 − 19
cos2α = 89
cosα = 2√23
dane
b = 5
sinα = 13
sin2α + cos2α = 1
cos2α = 1 − sin2α
cos2α = 1 − 19
cos2α = 89
cosα = 2√23
| sinα | √2 | |||
tgα = | = | |||
| cosα | 6 |
| a | √2 | ||
= tgα = | |||
| b | 6 |
| b√2 | 5√2 | |||
a = | = | |||
| 6 | 6 |
| a*b | 25√2 | |||
P= | = | |||
| 2 | 12 |

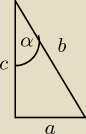 wzór ogólny to Sinα= ab
a więc jeśli w zadaniu jest że sinα=13
czyli ab=13 stąd wiemy że a=1, b=3, c=5 (także jest podane w zadaniu)
Liczymy pole:
wzór ogólny a*h2
w naszym przypadku c*a2=5*12=52=2,5
odp. Pole tego trójkąta wynosi 2.5cm2
wzór ogólny to Sinα= ab
a więc jeśli w zadaniu jest że sinα=13
czyli ab=13 stąd wiemy że a=1, b=3, c=5 (także jest podane w zadaniu)
Liczymy pole:
wzór ogólny a*h2
w naszym przypadku c*a2=5*12=52=2,5
odp. Pole tego trójkąta wynosi 2.5cm2


| 5√2 | ||
a = | ||
| 4 |
| a*b | 25√2 | |||
P = | = | |||
| 2 | 8 |
| 1 | ||
Lipas a skad wiesz ze ten trojkat ma boki 1,3,5? przeciez sinα= | moze tez doczyc | |
| 3 |
| 3 | 1 | |||
takich bokow 3,9 sinα= | = | |||
| 9 | 3 |
| 1 | ||
P= | * 5 * U{5√2{4} | |
| 2 |
| 5√2 | ||
x= | ||
| 4 |
| 1 | 5√2 | |||
P= | * 5 * | |||
| 2 | 4 |
| 25√2 | ||
P= | ||
| 8 |