Oblicz długość boku AD przedstawionego na rysunku czworkąta ABCD.
Jattamanka:
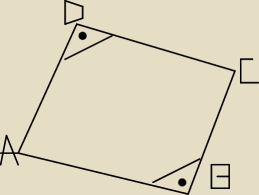
Oblicz długość boku AD przedstawionego na rysunku czworkąta ABCD.
AB = 5
√2
BC = 5
√2
CD = 6
√2
31 mar 17:21
bart: AD=BC bo skoro przeciwlegle katy sa proste to pozostale dwa tez musza byc proste. Co za tym
idzie to figura ta jest prostokatem o dwoch parach bokow rownoleglych o tej samej dlugosci.
31 mar 17:23
Jattamanka: nie może tak wyjść bo te boki obok siebie AB i BC są tej samej miary...
31 mar 20:22
Jattamanka: Dobra już wiem... : ppp
Więc daje rozwiązanie dla kogoś kto będzie tego może kiedyś potrzebował:
Przeciwległe kąty są proste więc można poprowadzić przekątną od wierzchołka A do C.
Wtedy wyliczamy pitagorasem:
("x" nazwałam przekątną)
(5
√2)
2+(5
√2)
2=x
2
(25*2)+(25*2)=x
2
50+50=x
2
100=x
2
x=10
Mamy więc przekątną AC = 10, dzięki niej znowu można wyliczyć z pitagorasa, tym razem szukany
bok |AD|. (We wzorze nazwałam go "y")
(6
√2)
2+y
2=10
2
(36*2)+y
2=100
72+y
2=100
y
2=100−72
y
2=28
y=2
√7
Więc nasz bok |AD| = 2
√7
; DDD
31 mar 20:58