hm Ania: .punkt b=(−1,9)nalezy do okregu stycznego z osia Ox w pkt A=(2,0).Wyznacz rownanie tego okregu.

M:

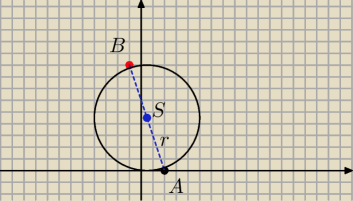
Luna : A=(2,0) B=(−1.9) Współrzedne punktu S środka odcinka AB

	2+(−1)
xS=
	2

	1
xs=
	2

	0+9
ys=
	2

	9
ys=
	2

	1		9
S=(		,
	2		2

	1
r=		|AB|
	2

	1
r=		√(−1−2)2+(9−0)2
	2

	1
r=		√90
	2

	1
r=		3√10
	2

Równanie okręgu

	1		9		90
(x−		)2+(y−		)2=
	2		2		4

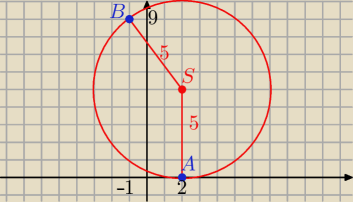Mania: S nie jest środkiem odcinka AB ! ! S=(2,r) i |BS|=r (2+1)²+(r−9)²=r² 18r=90 ⇒ r=5 S=(2,5) , r=5 o: (x−2)²+(y−5)²=25