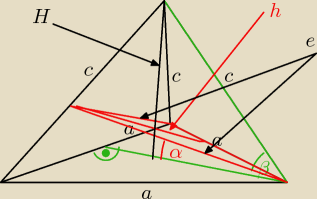
HELLLLLLLLP TOmek: Stereometria − poziom "prawie hardcore" Krawędź podstawy ostrosłupa prawidłowego trójkątnego ma długosc a. Krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem β. Ostrosłup ten przecięto płaszczyzną przechodzącą przez krawędź podstawy nachyloną do płaszczyzny podstawy pod kątem α. Oblicz pole otrzymanego przekroju to co zrobiłem to obrazek i zero pomyslu, myslałem o tw. cos, ale dupa pomozcie, prosze

Godzio : Spróbuję pomóc, ale może mi to trochę zająć Jeszcze rysunek trochę lepszy zrobię także bądź cierpliwy

Eta: https://matematykaszkolna.pl/forum/88479.html

Eta:

TOmek: Eta, nic mi te zadanie nie wniosło, bo tam przekroj jest pod kątem 90

Eta: Dobrze się przyjrzyj ......... to jest to samo zadanie , tylko są dane liczbowe To Ty masz zauważyć ,że ten trójkąt jest prostokątny

TOmek: dla mnie nie da sie udowodnic ,ze to ten przekroj jest prostokątny...

TOmek: to są juz koncowe zadnia kiełbasy, wiec nad jednym sie siedzi gdzies 1h−1,5h

Eta: To nie przekrój jest trójkątem prostokątnym, tylko wysokość przekroju i wysokość podstawy i część odcinka na krawędzi bocznej tworzą trójkąt prostokątny Zobacz co napisałam w poście Miłosz

TOmek: no ,ale tam mamy podane kąty a tu jakies α,β α może sie równac czemukolwiek, rozumiem gdyby krawedz boczna równała sie krawędzi podstawy.. ;0 ale tak nie jest i tego nie potrafie rozwiązac, zobaczymy, bo moze Godzio zrobi

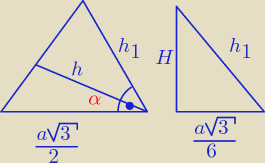Godzio : H − wysokość ostrosłupa h − wysokość szukanego przekroju h₁ − wysokość ściany bocznej

	H		a√3
tgβ =		⇒ H =		tgβ
	2   a√3   * 3   2		3

	a√3
h12 = H2 + (		)2
	6

	a2		a2
h12 =		tg2β +
	3		12

	4tg2β + 1
h12 = a2 *
	12

	√12tg2β + 3
h1 = a *
	6

a√3		1		h1 * a√3
	* h * sinα +		h * h1 * sin(90 − α) =
4		2		4

√3		√12tg2β + 3		a√4tg2β + 1
	* h * sinα + h *		cosα =
2		6		4

	3a√4tg2β + 1
h(3√3sinα + √12tg2β + 3cosα) =
	2

	3a√4tg2β + 1
h =
	6√3sinα + 2√12tg2β + 3cosα

	ah		3a2√4tg2β + 1
Pp =		=
	2		12√3sinα + 4√12tg2β + 3cosα

Możliwe ?

TOmek: jak Ty sobie z tym nie dajesz rady, to ja rezygnuje, to przewyzsza poziom matury roz. 5 razy xDD

	a2√3		sinβ
Godzio załamie Cię wynik to:		*
	4		sin(α+β)

Godzio : hmmm może dałoby się to przekształcić do tego wyniku ale to dopiero byłaby rzeźnia

Godzio : Zaraz spróbuję

TOmek: niee, bez przesady, ja Ufam Ci ,ze dobrze zrobiłes

TOmek: dla mnie najwazniejszy jest Twój pomysl rozwiązania tego zadania

Godzio : Wiesz co, musiałem się w rachunkach pomylić, zaraz poszukam błędu bo wynik jest w miarę podobny do tego co Ty masz

Eta: Ajjjjjjjj sorry , nie wiem czemu zobaczyłam kąty 30^o i 60^o zamiast α i β pewnie dlatego ,że u Miłosza takie były

TOmek: własnie sie dziwiłem Eto, co Ty mi wkręcasz , Godzio nie musisz przepisywać tutaj przeklształcenia, ja znam CIebie jestes zawzięty, zrób sobie na spokojnie na domowej kartce dla spokoju

Godzio : Za nic nie chce mi wyjść tak jak w odpowiedzi , a błędu w rozumowaniu też nie widzę

TOmek: sprawdziłem jeszcze raz dla spokoju wynik i dobrze przepisałem. Godzio gdzie dokładnie idziesz, polibuda we Wrocku, kiedys słyszałem a mozesz zdrawdzić kierunek? chyba ,ze nie chcesz to zrozumiem

kamis: Rozwiązanie: http://www.matematyka.pl/196527.htm

Godzio : TOmek jestem głupi jak but, a zadanie jest proste jak barszcz Zaraz pokaże

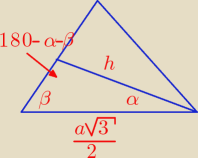Godzio : Dopiero teraz wpadłem że przecież tam jest kąt β ... sin(180 − (α + β)) = sin(α + β) Z tw. sin:

h		a√3   2
	=
sinβ		sin(α + β)

	a√3sinβ
h =
	2sin(α + β)

	ah		a2√3		sinβ
P =		=		*
	2		4		sin(α + β)

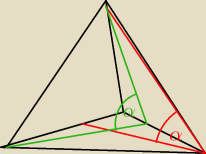TOmek: takie pytanko trzymając sie treści zadania, czy powyzszy rysunek u góry jest poprawny "zielone to dodane moje−>pytanie, czy α=α w tym przypadku" Krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem β Wydaje mi sie ,ze na 100procent NIE,ale chce byćpewny

TOmek: NIE, nie ,nie ma tego oczywistego pytania Jeszcze raz Dziekuej Godzio

Godzio : Nie są takie same

TOmek: danke