POMOCY ! Miłosz: Proszę o pomoc ambitnych Dany jest ostrosłup prawidłowy trójkątny. Krawędź podstawy tego trójkąta jest równa 12, krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem o mierze 60 stopni. a) Wyznacz pole przekroju ostrosłupa płaszczyzną przechodzącą przez krawędź podstawy i nachyloną do niej pod kątem o mierze 30 stopni. b) Wyznacz cosinus kąta ściany bocznej przy podstawie tego ostrosłupa. Może ktoś pomóc mi wykonać rysunek do tego zadania? Gdyż nie wiem czy dobrze rozumuje ten przekrój bo wychodzi mi pole jego 36√2 a w odpowiedzi jest 54

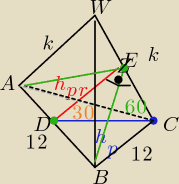
Eta: Witam Odp: P(przekroju)= 54 jest prawidłowa zauważ ,że wysokość przekroju i wysokość podstawy tworzą trójkąt prostokątny bo miara kąta między krawędzią boczną a wysokością podstawy = 60^o i miara kąta między wysokościa przekroju i wysokością podstawy = 30^o to trójkąt DEC jest prostokątny i teraz już prosto: h_p= 6√3 to h(przekr.) = U{6√3}*√3}{2}= 9

	12*9
P(przekroju AEB)=		= 54
	2

Eta: Poprawiam zapis:

	6√3*√3
h(przekroju) =		= 9
	2

ansz: eta Ty mature zdajesz?