równanie z parametrem gabi: UPRZEJMIE PROSZĘ O WSKAZÓWKI JAK TO ROZWIĄZAĆ Znaleźć zbiór wszystkich rzeczywistych wartości parametru rzeczywistego m., dla których suma rzeczywistych pierwiastków równania 4x⁴+4m(x²+1)−3=0 jest mniejsza od sumy kwadratów tych pierwiastków .

Jack: Wzory Viete'a w takiej nierówności: x₁+x₂<x₁²+x₂² gdzie x₁²+x₂²=(x₁+x₂)²−2x₁x₂

gabi: jako że to jest równanie podwójnie kwadratowe to muszę podstawić zmienną t pod x²?

Jack: oczywiście, ponadto x²=t, wiec t≥0.

gabi: t=x² t≥0 4t²+4mt+4m−3=0 Δ=16m²−4*4(4m−3)=16m²−64m+48=4m²−16+12=m²−4m+3 Δ_m=16−4*3=16−12=4 √Δ=2

	4−2
m1=		=1
	2

	4+2
m2=		=3
	2

i co dalej?

mac: Wzory VIETE'A

	b
x1 + x2 = −
	a

	−4m
x1 + x2 =		= −m
	4

	c
x1 * x2 =
	a

	4m − 3
x1 * x2 =
	4

Otrzymane wynik podstawiasz do tego do napisał Jack która klasa jesteś ?

ICSP: pamiętamy oczywiście o tym że Δ ≥0

prosze o pomoc...: iscp pomozesz

ICSP: nie mam czasu za dużo liczenia.

gabi: 2 lo m∊(−∞,1>∪<3,∞)

	4m−3
−m<m2+
	2

	3
m2+3m−		>0
	2

	3
Δ=9+4*		=9+6=15
	2

√Δ=√15

	−3−√15
m1=
	2

	−3+√15
m2=
	2

gabi: tylko że to będzie jeden kwadrat rozwalony dopiero..

gabi: nie wiem dobrze?

gabi: może ktoś mnie sprawdzić?

mac: Oj chyba nie Też jestem w drugiej LO

	2(m−3)
−m < m2 −
	4

Sprawdź znaki, i na końcu dla ułatwienia możesz pomnożyć przez dwójkę

gabi:

	2(4m−3))
−m<m2−
	4

to jest dobrze ale coś mi nie pasuje mam takie odpowiedzi do wyboru:

	3
a) m∊(−∞,		)
	4

b)m∊(∞,1>∪<3,+∞) c)m∊(0,1)

	3
d)m∊(0,		)
	4

mac: no a jak myślisz? Miałaś chyba Wzory Viete'a w pierwszej klasie? ja obstawiam b) − o ile nigdzie się w znaku nie pomyliłem , co jest bardzo prawdopodobne

gabi: miałam ale średnio do dziś je rozumiem. no to z tego mi wyszło to wyżej. ale jakoś dziwnie..

mac: Zaraz to gebi rozpisze ale wpierw dokończe zadanie z matmy

gabi: ok dzięki

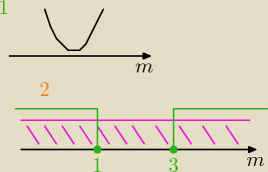
mac: Tak jak wspominałem jak wszystko powyżej poprawnie obliczone i nie ma błędów w znakach to:

	2(m − 3)
−m < m2 −
	4

	(m − 3)
−m < m2 −		/ *2
	2

−2m < 2m² − (m − 3) 0 < 2m² + 2m − m + 3 2m² + m + 3 > 0 Δ < 0, natomiast a > 0, więc: m∊R (1 rysunek) Teraz łączymy te dwa warunki(2 rysunek) − część wspólna to: m∊(−∞, 1>U<3, +∞)

gabi: dziękuję

mac: Jak coś nie jasne to pisz

gabi: jedna rzecz dlaczego Δ<0 i czym jest a>0

mac: Miałaś raczej w pierwszej klasie nierówności prawda ? Już tłumaczę: dla nierówności: 2m² + m + 3 > 0 Liczymy Δ = 1 − 24 = − 23 < 0 I jak mamy, że delta ujemna patrzymy tylko na znak przy współczynniku a czy taki sam znak ma (dodatnią wartość czy ujemną) jak znak nierówności Tutaj masz podobny przykład − https://matematykaszkolna.pl/strona/103.html A z jakiego miasteczka pochodzisz jak wolno spytać ?

gabi: lublin.

	4m−3
tylko jedna rzecz mi się nie zgadza jak liczyłeś x1*x2 to Ci wyszło
	4

	2(m−3)
później jak podstawiasz masz
	4

	2(4m−3)
a nie powinno być		?
	4

gabi: tamto rozumiem dzięki.

mac: Mój błąd, dobrze że sprawdzasz

	2(4m − 3)
−m < m2 −
	4

	(4m − 3)
−m < m2 −		/*2
	2

−2m < 2m² − (4m − 3) 2m² + 2m − 4m + 3 > 0 2m² − 2m + 3 > 0 Δ = 4 − 24 = −20 < 0 Czyli nadal ok

gabi: dobra zgadza się, dzięki jeszcze raz.

mac:

dziuba: mac pomożesz?

mac: Niestety nie miałem jeszcze logarytmów

dziuba: dzięki za chęci