WYZNACZ DZIEDZINE error demotywator.: WYZNACZ DZIEDZINE d

	4x + 2
f(x) =
	√x2 − 1

Wychodzi mi x > badz rowne 1 wiec D : R / <1 ; + nieskonczonosc) w odpowiedzi jest (− nieskonczonosci ; −1> U <1 ; + nieskonczonosci) Dlaczego

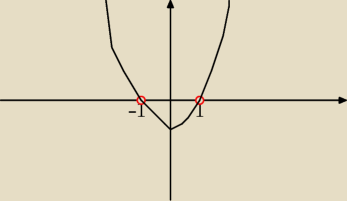
maturzysta: x² − 1 > 0 (x − 1)(x + 1) > 0 x∊(−∞, −1)U(1, +∞) Wyrażenie pod pierwiastkiem nie może być: x ≥ 0, tylko samo x > 0

maturzysta: Uzupełnienie: Wyrażenie pod pierwiastkiem nie może być x≥0 KIEDY JEST W MIANOWNIKU, wtedy jest x> 0

Eta: x²−1 jest pod pierwiastkiem i w mianowniku zatem: D_f: x²−1 >0 (x−1)(x+1) >0 => x€ (−∞, −1) U (1, ∞) przedziały muszą być obustronnie otwarte

demotywator.: Dzieki wielkie juz wiem Ale mam lekki zamet w kilku innych zadaniach

	2		2
f(x) =		+
	x + 2		(x+2)2

	1
oraz f(x) = √x−4 +
	√x−4

maturzysta: b) x − 4 ≥ 0 ⋀ x − 4 >0 a) D = R − {−2}

Eta: 1/ tylko mainowniki ≠0 => D_f = R \ {−2} 2/ tu masz pierwiastek ( z tego samego wyrażenia) i do tego w mianowniku, zatem x−4 >0 => x > 4 D_f= ( 4, ∞)

demotywator.: to dlaczego nawiasy tutaj sa inne niż tlumaczysz? https://matematykaszkolna.pl/strona/34.html

maturzysta: Bo jest w mianowniku a więc NIE MOŻE BYĆ ZEREM dlatego samo, x > 0 A ten przykład co podałeś nie jest w mianowniku

demotywator.: Spoko, dzieki a jescze cos takiego : f(x) = √x − √−x

maturzysta: Również: x ≥ 0 ⋀ −x ≥ 0

demotywator.: 100 krotne dzieki

maturzysta: ⋀ − to część wspólna −x ≥ 0 / * (−1) x ≤ 0 [..]

demotywator.: dzieki, obryje sie tego i ide w funkcje kwadratową.