 y=3(x−4)2 postać kanoniczna f. kwadratowej
a=3 p=4 q=0
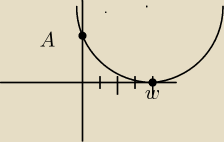
W=(p,q) ten punkt to wierzchołek paraboli
W=(4,0)
3(x−4)2=0 /3
(x−4)2=0
x−4=0
x=4 miejsce zerowe funkcji jest ono podwójnym pierwiastkiem
a=3 a>0 ramiona paraboli skierowane do góry
y=3(x−4)2
x=0
y=3(0−4)2
y=3*16
y=48
A=(0,48)
y=3(x−4)2 postać kanoniczna f. kwadratowej
a=3 p=4 q=0
W=(p,q) ten punkt to wierzchołek paraboli
W=(4,0)
3(x−4)2=0 /3
(x−4)2=0
x−4=0
x=4 miejsce zerowe funkcji jest ono podwójnym pierwiastkiem
a=3 a>0 ramiona paraboli skierowane do góry
y=3(x−4)2
x=0
y=3(0−4)2
y=3*16
y=48
A=(0,48)
 y=3x2+3
a=3 b=0 c=3
Δ=b2−4ac=02−4*3*3=−36
Δ<0 brak miejsc zerowych
x=0
y=3*02+3
y=3
A=(0,3)
a=3 a>0 zatem ramiona paraboli skierowane do góry
y=3x2+3
a=3 b=0 c=3
Δ=b2−4ac=02−4*3*3=−36
Δ<0 brak miejsc zerowych
x=0
y=3*02+3
y=3
A=(0,3)
a=3 a>0 zatem ramiona paraboli skierowane do góry
| −b | −0 | |||
p= | = | =0 | ||
| 2a | 2*3 |
| −Δ | 36 | 36 | ||||
q= | = | = | =3 | |||
| 4a | 4*3 | 12 |