Zadanie Godzio : Chciałbym się dowiedzieć jak można znaleźć punkt na krzywej y = √4x − x² dla którego

	5
odległość punktu P(		,1) jest najmniejsza.
	2

Grześ: jakby dobrze się zastanowić, to moznaby policzyć pochodną w jakimś punkcie x₀ i wyznaczyć drugą wspł. tego punktu. Powstały odcinek między pkt. styczności a pkt. P ma najmniejszą odległośc dla kąta prostego między tymi prostymi(odcinkiem a pochodną w punkcie) Czy dobrze myslę Może dałoby radę coś z tym zrobić

Grześ: co o tym sądzisz

Godzio : Ale wolałbym jakimś sposobem bardziej licealnym chyba, że się nie da

Grześ: to chyba pierwsze co wpadło mi do głowy szczerze, to nie wiem naprawdę.... może jakiś trójkąt da się ułożyć hmm..

załamany :( : a kminiłes cos z katem prostym badz czyms podobnym chociaz nie wiem czy sie da

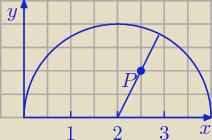
Godzio : A teraz tak pomyślałem, czy odległość nie będzie najmniejsza jeśli poprowadzi się promień przez punkt P ?

Godzio :

	5
S(2,0) P(		,1)
	2

0 = 2a + b

	5
1 =		a + b
	2

	1
−1 = −		a
	2

a = 2 b = −4 y = 2x − 4 2x − 4 = √4x − x² 4x² − 16x + 16 = 4x − x²

	2
5x2 − 20x + 16 = 0 ⇒ x = 2 +		√5
	5

Nawet by się z odpowiedzią zgadzało Tylko pytanie czy to trzeba uzasadnić czy to jest na tyle oczywiste że nie trzeba hmmm