zrób mati: funkcja f(x)=(m−3)x−1 nie ma miejsc zerowych dla a: m<3, b: m=3, c: m>3, d: m≠3

Ireneusz: Aby nie miała miejsc zerowych musi być to funkcja stała, więc m−3=0 −> m=3.

mati: zbiorem rozwiązań nierównosci −2(x−1)(x=3)>0 jest a: (−∞;−3)∪(1;∞), b: (−1;3), c:(−∞;−1)(3;∞), d:(−3;1)

Ireneusz: Na pewno dobrze przepisałeś nierówność x=3 nie powinno być x+3? Jeśli tak to zbiorem będzie d

jajajaja: no x+3 sorki

jajajaja: a jak to zrobic

Ireneusz: Rysujesz parabolę o miejscach zerowych −3 i 1. Parabola ma minus, więc ramiona skierowane w dół i patrzysz w jakim przedziale parabola jest "nad osią".

jajajaja: i tak mi nic nie wyszlo

Ireneusz: Dlaczego?

jajajaja: no skad wiesz ze to akurat ten zbior

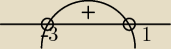
Ireneusz: Funkcja ma być tylko większa od zera, więc kółeczka są niezamalowane. Więc patrzysz gdzie funkcja przyjmuje wartości dodatnie(zaznaczyłem Ci je plusem).

jajajaja: a z innymi zbiorami nie wyjdzie dlaczego

Ireneusz: (−∞;−3)∪(1;∞) ten zbiór były gdyby zadanie tak wyglądało −2(x−1)(x+3)<0 (−1;3) tu chodzi, że uczeń nie wie jak znaleźć miejsce zerowe (zapomina o minusie) c:(−∞;−1)(3;∞) tu tak samo zapomina o minusie i −2(x−1)(x+3)<0