Planimetria Angel: 1. W trójkącie ABC o polu 20cm2 na boku AB obrano punkt D, taki że |AD| = 1/4 |AB|, a na boku BC − punkt E taki, że |BE| = 1/5 |BC|. Oblicz pole prostokąta. 2. Odcinek poprowadzony z jednego z wierzchołków prostokąta prostopadle do przekątnej dzeli tę przekątną na dwa odcinki o długościach 4 i 9. Oblicz pole prostokąta. 3. Oblicz pole rombu o kącie ostrym α, wiedząc że prosimień okręgu wpisanego w ten romb równa się r. Z góry dziękuję za pomoc

Angel: 2 już zrobiłam, z 1 i 3 nie mogę dać rady

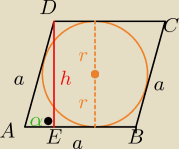
Eta: 3/ h= 2r P= a*h

2r
	= sinα
a

	2r
a=
	sinα

	4r2
P=
	sinα

Eta: 1/ jakiego prostokąta? ......... nie napisałaś

Angel: Heh zrobiłam 3, a tu rozwiązane xd w pierwszym ma być oblicz pole trójkąta BDE

Angel: help z 1

Eta:

	1
P(ΔABC) =		*|AB|*|BC|
	2

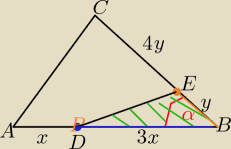
	1
		*4x*5y*sinα= 20 => 10xy*sinα= 20 => x*y*sinα= 2
	2

	1		3		3
P(ΔDBE) =		*3x*y*sinα=		*x*y*sinα=		*2= 3 [ j2]
	2		2		2

Angel: Dziękuję za pomoc, tylko nie rozumiem dlaczego liczysz pole trójkąta ABC jakby był prostokątny.

Eta: Jaki prostokątny?

	1
P(Δ) =		iloczynu długości dwu boków *sin kąta między nimi
	2

Eta: https://matematykaszkolna.pl/strona/503.html

Angel: Tak tak wiem, tylko w P(ΔABC) =1/2*|AB|*|BC| brakowało sinα i sie zastanawiałam

Angel: Prosiłabym również o pomoc w tym, w ogóle nie rozumiem treści zadania. =/ Dany jest kwadrat o boku a wpisany w okrąg. Oblicz długość boku kwadratu, którego dwa wierzchołki należą do łuku okręgu, dwa pozostałe do jednego z boków kwadratu.

Angel: up