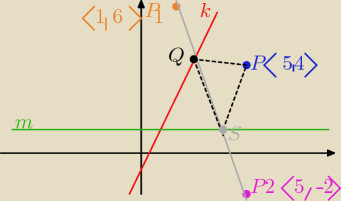
Jack: Jak wyznaczyć punkt przecięcia się dwóch prostych ? Chociaż nie... Bo w zasadzie nie znam nawet równania drugiej prostej xd. Mam takie zadanie: Dana jest prosta k o równaniu y=2x−1, prosta m o równaniu y=1 i punkt P(5,4). a) wyznacz współrzędne punktów P1 P2, wiedząc, że P1 jest obrazem punktu P w symetrii osowej względem prostej k, a P2 jest obrazem punktu P w symetrii osiowej względem prostej m. b) Wyznacz punkty Q, S przecięcia prostej P1,P2 odpowiednio z prostą k i prostą m. c) Wykaż, że spośród wszystkich tójkątów, których jednym z wierzchołków jest punkt P, drugim wierzchołkiem jest punkt należący do prostej k, a trzecim punkt należący do prostej m, najmniejszy obwód ma trójkąt PQS. (nad tym jeszcze nie myślałem, zależy mi najpierw na a,b punktach, ale zrobiłem też rysunek do tego ). Z rysunku to dam radę odczytać, ale jak to wyliczyć? Bo jak dostanę jakieś ułamkowe liczby to się wyłożę...

Jack: Tak patrzę teraz i... Chyba punkt P1 i P2 jestem w stanie wyliczyć. No bo w sumie mogę policzyć odległość punktu P od prostej m i od prostej k. Wtedy powinienem dać radę wyliczyć punkty P1 i P2, tylko, że trzeba by je policzyć dla wektoru przeciwnego, bo będą one szły pod kątem prostym obie... Dobrze myślę ?

Jack: Proszę o pomoc...

Jack: Kolejny raz odświeżam

Tomek.Noah: Pomoge ale dopiero gdzies wieczorkiem uwazam ze jest zadanie do zrobienia wystarczy odswierzyc pare wzorkow Cierpliwosci

Jack:

Jack: okej, poczekam, nic innego mi nie pozostało.

dero2005: 1) wyznaczasz punkt P₁ − prosta prostopadła do k i przechodząca przez punkt P a = −¹₂ y = a(x−x_P)+y_P y = −¹₂(x−5)+4 y = −¹₂x + ¹³₂ − punkt C przecięcia tej prostej z prostą k −¹₂x +¹³₂ = 2x−1 −x+13 = 4x−2 −x−4x = −2−13 −5x = −15 x = 3 y = 2x−1 = 6−1 = 5 C = (3, 5) −liczymy punkt P₁

	xP+xP1		yP+yP1
C=(		,		) = (3, 5)
	2		2

5+xP1
	= 3
2

x_P1 = 1

4+yP1
	= 4
2

y_P1 = 6 P₁( 1, 6) 2) wyznaczasz punkt P₂ − prosta prostopadla do m i przechodząca przez punkt P(5,4) m, y = 1 prosta pozioma x = 5 prosta pionowa − punkt przecięcia prostych D D = (5, 1) − liczymy punkt P₂

	xP+xP2		yP+yP2
D = (		,		) = (5, 1)
	2		2

	5+xP2
		= 5 xP2 = 5
	2

4+yP2
	= 1 yp2 = −2
2

P₂ = (5, −2) 3) wyznaczamy prostą zawierającą odcinek |P₁P₂|

	yP2−yP1		−2−6		−8
a =		=		=		= −2
	xP1−xP1		5−1		4

y = a(x−x_P1)+y_P1 y = −2(x−1)+6 y = −2x + 8 4) wyznaczamy punkt Q przecięcia się z prostą k −2x+8 = 2x−1 −2x−2x = −1−8 −4x = −9 x = ⁹₄ y = −2*⁹₄+8 = ¹⁴₄ Q = (⁹₄ , ¹⁴₄) 5) wyznaczamy punkt S przecięcia z prostą m y = 1 y = −2x+8 −2x+8 = 1 −2x = 1−8 −2x = −7 x = ⁷₂ y = 1 S=( ⁷₂ , 1)

Jack: Dziękuję