prosze o pomoc hania009: prosze o pomoc ! znając długości środkowych trójkąta znajdź długości boków tego trójkąta

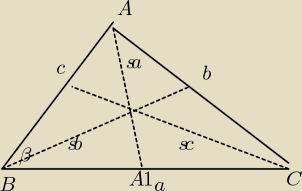
AS: ΔAA1B − z tw. cosinusów sa² = c² + (a/2)² − 2*c*(a/2)*cos(β) ΔABC − z tw. cosinusów b² = a² + c² − 2*a*c*cos(β) Pierwsze równanie mnożę przez 2, drugie przez −1 2*sa² = 2*a² + a²/2 − 2*a*c*cos(β) −b² = −a² − c² + 2*a*c*cos(β) Stronami dodaję oba równania i porządkuję 4*sa² = 2*b² + 2*c² − a² Podobnie dla pozostałych środkowych 4*sb² = 2*c² + 2*a² − b² 4*sc² = 2*a² + 2*b² − c² Uzyskaliśmy układ trzech równań z trzema niewiadomymi a,b i c