tago: W pewnym trójkącie prostokątnym suma cosinusów kątów ostrych jest równa 2√3/ 3 . Oblicz iloczyn sinusów tych kątów.

Krecik:

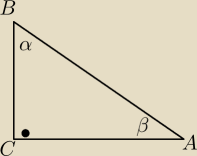
Metis: Trójkąt ABC − dowolny trójkąt prostokątny cosinus liczba, która określa stosunek długości przyprostokątnej przyległej do kąta i przeciwprostokątnej Z rysunku:

	BC		CA
cos α =		i cos β =
	AB		AB

Z warunków zadania:

	2√3
cos α + cos β =		, podstawiam
	3

BC		CA		2√3
	+		=
AB		AB		3

AC+BC		2√3
	=
AB		3

Sinus liczba, która określa stosunek długości przyprostokątnej leząca naprzeciwko kąta i przeciwprostokątnej Sinusy w naszym trójkącie:

	CA
sin α =
	BA

	BC
sin β =
	BA

Z zadania:

	CA		BC
sin α * sin β =		*
	BA		BA

AC+BC		2√3
	=		− podnieś to do kwadratu i wyciagnij wnioski...
AB		3

5-latek: Metis najedz sobie myszka na date i zobacz z ktorego roku jest to zadanie

5-latek: A krecik to archeolog

Metis:

pigor: ... .W pewnym trójkącie prostokątnym suma cosinusów kątów ostrych jest równa ²₃√3. Oblicz iloczyn sinusów tych kątów. −−−−−−−−−−−−−−−−−−−−−−−− no to do ... "szuflady" przy standardowych oznaczeniach elementów Δ prostokątnego np. tak: cosα+cosβ= ²₃√3 ⇔ ^b_c+^a_c = ²₃√3 ⇔ ⇔ ^b+a_c = ²₃√3 /² ⇒

	b2+a2+2ab		c2+2ab
⇒		= 43 ⇔		= 43 ⇔
	c2		c2

	2ab
⇔ 1+		= 43 ⇔ 2 abcc = 13 /:2 ⇔
	c2

⇔ ^a_c*^b_c = ¹₆ ⇒ sinα* sinβ = ¹₆ . ...

mono: No to ja ....... bez szufladki cosα=sinβ i cosβ= sinα

	2√3		2√3
cosα+cosβ=		⇒cosα+sinα=		/2
	3		3

	4		4		1
cos2α+2cosα*sinα+sin2α=		⇒ 2sinβ*sinα=		−1=
	3		3		3

	1
to sinα*sinβ=
	6