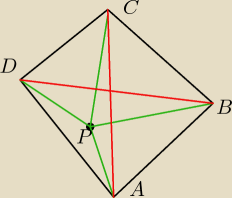
Jack: Wykaż, że suma odległości dowolnego punktu płaszczyzny od wierzchołków czworokąta wypukłego jest nie mniejsze niż suma długości jego przekątnych. Czy to zadanie może być zrobione w ten sposób ? : zał: |PA|+|PB|+|PC|+|PD|≥|AC|+|DB| Zauważam, że na rysunku powstały trójkąty: ΔPDB oraz ΔPAC Z twierdzenia o zbudowaniu dowolnego trójkąta wiemy, że aby stworzyć trójkąt musi być spełniony warunek: Suma dwóch krótszych boków tego trójkąta musi dać więcej niż długość trzeciego boku. Na podstawie tego twierdzenia : 1) ΔPAC może być stworzony wtedy i tylko wtedy, gdy : |PA|+|PC|>|AC| − a skoro powstał to w istocie tak jest... 2) ΔPBD może być stworzony wtedy i tylko wtedy, gdy : |PD|+|PB|>|BC| − a skoro powstał to tak musi być... No więc skoro |PA|+|PC|>|AC| i |PD|+|PB|>|BC| to twierdzenie: |PA|+|PB|+|PC|+|PD|≥|AC|+|DB| jest prawdziwe. Czy udowodniłem to ? Jest zadanie zrobione poprawnie ? Dodam, że jest to zadanie z matury rozszerzonej za 3 punkty.

Jack: 2) ΔPBD może być stworzony wtedy i tylko wtedy, gdy : |PD|+|PB|>|BD| − a skoro powstał to tak musi być... Wkradła się drobna literówka.

andre: godzia sie spytaj, S**

Jack: odświeżam...

kamis: Takie dowodzenie z pewnością wystarczy.

Godzio : Jest ok

Jack: Doskonale Dowartościowałem się Dziękuję

magdalena: dlaczego z 2 nierówności ...>... powstaje 1 nierówność ...≥... ?

Dominik: dodano je do siebie.

magdalena: czy nie należy rozważyć dodatkowego przypadku, że P leży na przecięciu się przekątnych? i wtedy wychodzi nam ta równość.