Przekątna kwadratu, równanie okręgu i zbiór nierówności Sarmata: Witam. Potrzebuje pomocy w czterech zadaniach. 1. Przekątna kwadratu ma długość 4. O ile procent wzrośnie pole kwadratu jeśli długość przekątnej zwiększymy o 40%? 2. Znajdź równanieokręgu o środku w punkcie P= (−1;1) stycznego do prostej o równaniu x=−2 3. Zbiorem rozwiązań nierówności −(x−5)(x+6)≥0 jest ? Prosiłbym o wyjaśnienie jak dojść do rozwiązania. 4. Stosunek długości boków trójkąta może być równy: A: 1:3:2 B: 2:5:7 C.7:5:3 D.4:5:1 I tutaj potrzebne uzasadnienie Będę bardzo wdzięczny za wszelką pomoc.

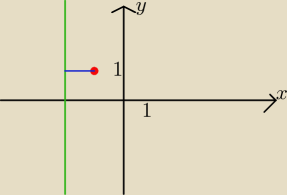
ICSP: zielony − prosta x = −2 czerwony − środek okręgu niebieski promień okręgu czyli odległość między prostą a punktem. Na oko widać że jest równy 1 (x+1)² + (y−1)² = 1

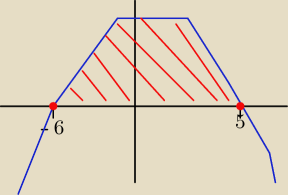
ICSP: −(x−5)(x+6)≥0 1. Liczę miejsca zerowe: −(x−5)(x+6) = 0 ⇔ x = 5 v x = −6 2. Zaznaczam te punkty na osi liczbowej i rysuję przybliżony wykres. Pamiętam o tym że współczynnik a jest <0 czyli parabola ma ramiona skierowane w dól Wiem że rysunek nie jest jakimś arcydziełem ale nie umiem rysować ładnie paraboli. Niebieski to wykres paraboli a czerwony rozwiązanie Zauważ że czerwone kropki są również na miejscach zerowych.

ICSP: Trójkąt możemy zbudować wtedy kiedy suma dwóch krótszych boków jest większa od boku największego. 1:3:2 1 + 2 = 3 3 >3 − jest to sprzeczne czyli trójkąt nie może mieć takiego stosunku boków. 2:5:7 2+5 = 7 7>7 − znowu sprzeczność . Robisz dalej tak samo.

Sarmata: Wow, dzięki. Jesteś wielki A dałbyś radę jeszcze z tym pierwszym?

ICSP:

	d2
Każdy kwadrat jest rombem: P =
	2

d₁ = 4 d₂ = 1,4 * 4 = 5,6 P₁ = 8 P₂ = 15,68

P2 − P1
	* 100% = 96%
P1

Sarmata: Kurcze, problem w tym że nie miałem takiego wzoru na lekcji i zaraz może się przyczepić.

ICSP: a wzór na przekątną kwadratu miałeś?

Sarmata: tak, a√2

Sarmata: a więc jak wykorzystać do tego pierwszego wzór na przekątną?

Sabin: a√2 = 4 wyliczasz a, wyliczasz pole potem zwiększasz o 40% przekątną, czyli b√2 = 4*1,4, wyliczasz b, wyliczasz nowe pole, liczysz stosunek