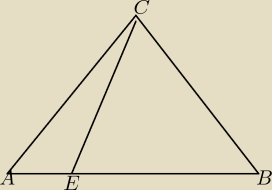
 W trójkącie równoramiennym ABC podstawa AB ma długość 20 cm. Punkt E należący do tej podstawy
dzieli ją w stosunku 1:4. Odcinek CE ma długość 10 cm. Oblicz obwód trójkąta ABC.
W trójkącie równoramiennym ABC podstawa AB ma długość 20 cm. Punkt E należący do tej podstawy
dzieli ją w stosunku 1:4. Odcinek CE ma długość 10 cm. Oblicz obwód trójkąta ABC.
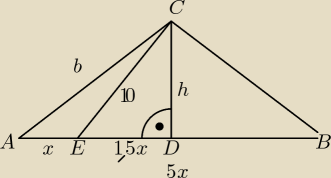 przyjmuję długość odcinka AE=x→długość odcinka AB=5x, czyli x=20/5=4 cm
ponieważ w Δ równobocznym wysokość opuszczona na podstawę dzieli ją na połowę (ramiona są
równe), to odcinek AD =12 AB, czyli 2,5x= 2,5*4=10 więc odc. ED=1,5x =1,5*4=6 cm
h obl. z ΔEDC→h=√102−62=√64=8 cm
z ΔADC obl. b,
b2=(AD)2+h2=
=b2=102+82=164
b=√164=√4*41=2√41 cm
obwód trójkąta=20+2*2√41=20+4√41=4(5+√41)cm
przyjmuję długość odcinka AE=x→długość odcinka AB=5x, czyli x=20/5=4 cm
ponieważ w Δ równobocznym wysokość opuszczona na podstawę dzieli ją na połowę (ramiona są
równe), to odcinek AD =12 AB, czyli 2,5x= 2,5*4=10 więc odc. ED=1,5x =1,5*4=6 cm
h obl. z ΔEDC→h=√102−62=√64=8 cm
z ΔADC obl. b,
b2=(AD)2+h2=
=b2=102+82=164
b=√164=√4*41=2√41 cm
obwód trójkąta=20+2*2√41=20+4√41=4(5+√41)cm