Rozwiąż nierówność (suma cosinusów) januszekm3: Jak rozwiązać nierówność: cos2x+cosx>0

dąlgdop: 1 − 2cos²x + cosx > 0 −2cos²x + cosx + 1 > 0 t = cosx −2t² + t + 1 > 0 Δ = 1 + 8 = 9 √Δ = 3

	−1 − 3
t1 =		= 1
	−4

	−1 + 3		1
t2 =		= −
	−4		2

	1
t∊(−		, 1)
	2

	1
t > −		∨ t < 1
	2

	1
cosx > −		∨ cosx < 1
	2

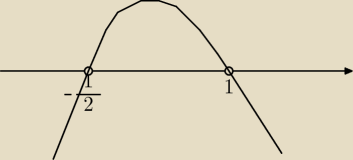
Teraz odczytaj z wykresu

Godzio: cos2x = 2cos²x − 1

januszekm3: Dzięki za pomoc, ale cox2x≠1 − 2cos²x, jak już to 2cos²x−1, wtedy pierwiastki t wychodzą −1 oraz 0.5

januszekm3: Godzio, wyprzedziłeś mnie

dąlgdop: Sorki Pomyliły się strony ale ciągniesz tak jak "robiłem"

januszekm3: Wychodzi piękny wynik, z sumy sinusów mamy paskudny przepis 4 przedziałów (...i...)lub(...i...), weź tu znajdź odpowiednie rozwiązanie :E Twój sposób jest banalny

dąlgdop:

	x + y		x − y
2cos		* cos
	2		2

	2x + x		2x − x		3		1
2cos		* cos		= 2cos		x * cos		x
	2		2		2		2

	3
1. 2cos		x > 0
	2

	1
2. cos		x > 0
	2

Proszę

januszekm3: Źle, bo jeszcze druga możliwość − oba czynniki iloczynu ujemne, wtedy też iloczyn będzie dodatni. 4 możliwości − dłuższa droga

dąlgdop: Masz może do tego odpowiedź? Bo widzę, że chyba to robiłeś na lekcji. To mam takie pytanie: według ciebie ile rozwiązań ma równanie cos2x + cosx = 0 tym samym sposobem?

januszekm3: Nie mam właśnie do tego odpowiedzi w podręczniku (w ogóle do żadnego przykładu z tego zadania). Gdybyśmy zrobili to na lekcji to bym tu nikogo nie pytał. Łatwo widać, że iloczyn będzie dodatni, gdy oba czynniki będą tego samego znaku. To mam takie pytanie: według ciebie ile rozwiązań ma równanie cos2x + cosx = 0 tym samym sposobem? To równanie ma nieskończenie wiele rozwiązań.

dąlgdop: cos2x + cosx = 0 Suma cos:

	3		1
2cos		x * cos		x = 0
	2		2

	3		1
(2cos		x) * (cos		x) = 0
	2		2

1^o

	3
2cos		x = 0 / : 2
	2

	3
cos		x = 0
	2

3		π
	x =		+ 2kπ / * 2
2		2

3x = π + 4kπ / : 3

	π		4kπ
x =		+		, k∊C
	3		3

2^o

	1
cos		x = 0
	2

1		π
	x =		+ 2kπ
2		2

	π
x =		+ kπ, k∊C
	4

Bardziej o takie rozwiązanie równania mi chodziło

dąlgdop: I podobnie rozwiązujesz tę nierówność tylko tam sprawa ma się z odczytywaniem trochę gorzej

januszekm3: W wykresu odpowiedź to będzie (−π/3+2kπ, π/3+2kπ) Tym 1 sposobem wyszło dopełnienie tego zbioru, czemu

januszekm3: Wiem, źle obrałem t

dąlgdop: Teoretycznie polecenie brzmiało aby rozwiązać tym drugim co napisałem (sam początkowo nie doczytałem)

januszekm3: Nic to, zadanie rozwiązane

dąlgdop: którym sposobem ?

januszekm3: Zamiana na 2cos²x−1

dąlgdop: Drugi lepszy

januszekm3: A gdzie tam, zresztą to bez różnicy