dziwne zadanie szybko: Dla trójkąta ABC iloczyn Sinα*cosβ jest równy ile W trójkącie dłuższa przyprostokątna, która leży przy kącie alfa ma dłuość 5. Innych danym nie ma.

szybko: jest na to jakis wzór

szybko: rozumiem, że cosβ = Sinα ale czy coś mi to daje?

bart: masz rysunek do tego nie ma innych danych

szybko: mam rysunek ale jak chcem tu narysowac to mi sie cos zacina wiec nie za bardzo moge. innych danych nie ma

szybko: sa jeszcze odpowiedzi 4 mozliwe a 4/29 b 10/29 c 25/29 d 1

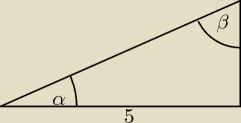
bart: takie cos?

szybko: tak dokladnie

szybko: i jak tam

szybko: nikt nie potrafi zrobic tego zadania?

ICSP: sinα * cosβ = sin²α Zacznijmy rozpatrywać po kolei

	4
a)
	29

	4		2
sin2α =		⇔ sinα =		. Specjalnie nie usuwam niewymierności z mianownika.
	29		√29

teraz sprawdzamy twierdzeniem pitagorasa czy zachodzi równość 2² + 5² = √29² ⇔ 4 + 25 = 29 ⇔ 29 = 29 Heh trafiłem za pierwszym razem

szybko: dzieki czyli bez podstawiania się nie da zrobić

ICSP: Pewnie sie da ale nie znam takiego sposobu.

Ajtek: Ja kombinuje, ale cały czas wychodzą mi tożsamości i chyba sobie odpuszczę .