ostro Minioo: Pilne Proszę o rozwiązanie... Podstawą ostrosłupa jest romb o boku długości a. Dwie przylegle sciany boczne ostrosłupa tworzą kąt o mierze 60 stopni i są prostopadłe do płaszczyzny podstawy. Oblicz objętość tego ostrosłupa, wiedząc, że najdłuższa krawedz boczna jest nachylona do płaszczyzny podstawy pod kątem 30 stopni.

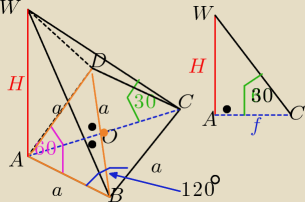
Eta: Witam miara kąta między ścianami prostopadłymi ABW i ADW wynosi 60^o co oznacza ,że miara kąta ostrego rombu = 60^o

	1		a2√3
V=		Pp*H , Pp= a2*sin60o =
	3		2

teraz pozostaje wyznaczyć długość H ( potrzebna jest do tego długość "f" ΔABD jest równoboczny o boku dł. "a" zatem IBD|= e= a

	1
|AO|=		f
	2

f²+e²= 4a² f²= a²= 4a² => f²=3a² to: f= a√3 z ΔACW :

	H
		= tg60o
	f

	√3
H= a√3*
	3

H= a

	a2√3		a3√3
V=		*a=		[j3]
	6		6

gosia: dłuższa przekątna graniastosłupa prawidłowego sześciokątnego ma długość 13 . oblicz pole powierzchni całkowitej tej bryły wiedząc że jej krótsza przekątna jest nachylona do płaszczyzny podstawy pod kątem 60 stopni