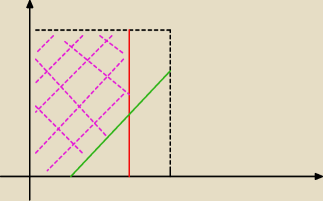
Prawdopodobieństwo graficzne Marcinek: Widzę, że Sabin działa, więc może uda mi się skorzystać z jego wiedzy po raz drugi Mam takie zadanie: W kwadratach [0,1]x[0,1] wybieramy losowo punkt (x,y). Załóżmy, że wszystkie wybory punktów są jednakowo prawdopodobne. Niech A będzie zdarzeniem losowym polegającym na tym, że x>y+0,3, natomiast B zdarzeniem losowym polegającym na tym, że x<0,7. Czy zdarzenia A i B są niezależne? Do tej pory udało mi się uzyskać coś, co pokazałem na obrazku. Dobrą drogą idę? Z góry dzięki za każde wskazówki!

Sabin: Tak, z tym ze pamietaj ze do pokazania niezaleznosci potrzebujesz p−twa P(A), P(B) oraz P(A∩B). P(A∩B) policz jako sume pol prostokata i trapezu, P(A) i P(B) sa prosciutkie.

Sabin: A nie, moment, to rozowe to nie jest wlasciwe pole. Ze zdarzenia A wychodzi y < x − 0,3, czyli jesli chcesz zaznaczyc P(A razy B) to zakreskowany powinien byc ten maly trojkat miedzy zielona a czerwona kreska.

Sabin: Mi wyszlo ze nie sa niezalezne, P(A razy B) = 0,08, zas P(A)P(B) = 0,1715

Marcinek: Tak, właśnie też pole trójkąta wyszło mi 0,08 Tylko jak Pan wyznaczył te P(A) i P(B)?

Sabin: P(A) − pole trojkata prostokatnego, przeciwprostokatna − zielona, przyprostokatne − odcinki bokow kwadratu. P(B) − pole prostokata ograniczonego czerwona kreska, osiami oraz odcinkami bokow kwadratu. I nie pan, 18 lat nie mam ale zeby mnie az tak postarzac...

Marcinek: Okej, już będę wiedział, dzięki za pomoc w kolejnym zadaniu! Chyba ten poziom wiedzy tak Cie postarza Pozdrawiam serdecznie!