pole trapezu... Anarion: Pole trapezu równoramiennego jest równe 36cm², a stosunek długości podstaw wynosi 1:2. Oblicz pola czterech trójkątów, na które dzielą ten trapez jego przekątne.

wicia:

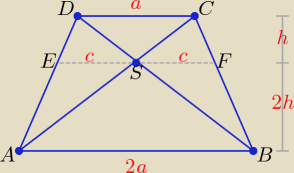
Bogdan: Przedstawiam jeden ze sposobów rozwiązania zadania. Odcinek równoległy do podstaw, przechodzący przez punkt przecięcia przekątnych i łączący ramiona trapezu ma długość równą średniej harmonicznej długości podstaw, czyli:

	2*2a*a		2
|EF| = 2c =		⇒ c =		a
	2a + a		3

	1		1
PABS =		*2a*2h = 2ah, PCDS =		ah,
	2		2

	1		1		3		2
PASD = PBCS = PASE + PESD =		c*2h +		c*h =		*		a*h = ah
	2		2		2		3

	1		9
Pole trapezu 36 = 2ah +		ah + ah + ah ⇒ 36 =		ah ⇒ ah = 8
	2		2

	1
PABS = 2*8 = 16, PCDS =		*8 = 4, PASD = PBCS = 8
	2

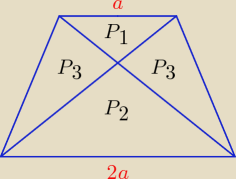Bogdan: Inny sposób.

	1
Skala podobieństwa trójkątów o polach P1 i P2 jest równa		,
	2

	P1		1
stąd		=		⇒ P2 = 4P1
	P2		4

Korzystamy z zależności: Pole trapezu P = (√P₁ + √P₂ )² = P₁ + 2√P₁*P₂ + P₂, P₃ = √P₁*P₂ 36 = P₁ + 2√P₁*4P₁ + 4P₁ ⇒ 36 = 5P₁ + 2*2P₁ ⇒ P₁ = 4 P₂ = 4*4 = 16, P₃ = √4*16 = 8

Eta: